ГДЗ по Геометрии 9 класс Номер 1113 Атанасян — Подробные Ответы

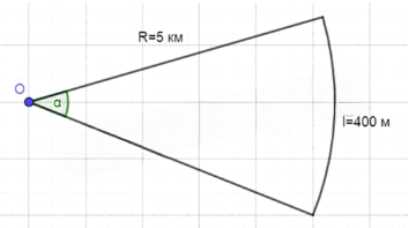
Радиус закругления пути железнодорожного полотна равен 5 км, а длина дуги закругления — 400 м. Какова градусная мера дуги закругления?

Дано: \(R = 5 \, \text{км}\), \(l = 400 \, \text{м}\).

Найти: \(\alpha\).

Решение:

1. Переведем длину дуги в километры:
\(l = 400 \, \text{м} = \frac{400}{1000} = 0{,}4 \, \text{км}\).

2. Используем формулу длины дуги:
\(l = \frac{\pi R \cdot \alpha}{180^\circ}\).

3. Выразим угол \(\alpha\):
\(\alpha = \frac{l \cdot 180^\circ}{\pi R}\).

4. Подставим значения:
\(\alpha = \frac{0{,}4 \cdot 180^\circ}{3{,}14 \cdot 5}\).

5. Вычислим:
\(\alpha \approx 4{,}35^\circ\).

Ответ: \(\alpha = 4^\circ 35’\).

Дано: \( R = 5 \, \text{км} \), \( l = 400 \, \text{м} \).

Найти: угол \(\alpha\).

Решение:

1. Переводим длину дуги из метров в километры, так как радиус задан в километрах.
\(
l = 400 \, \text{м} = \frac{400}{1000} = 0{,}4 \, \text{км}
\)

2. Используем формулу длины дуги окружности:
\(
l = \frac{\pi R \cdot \alpha}{180^\circ}
\)
где \( l \) — длина дуги, \( R \) — радиус окружности, \(\alpha\) — центральный угол в градусах.

3. Выразим угол \(\alpha\):
\(
\alpha = \frac{l \cdot 180^\circ}{\pi R}
\)

4. Подставляем известные значения в формулу:
\(
\alpha = \frac{0{,}4 \cdot 180^\circ}{3{,}14 \cdot 5}
\)

5. Выполняем вычисления:
\(
\alpha = \frac{72}{15{,}7} \approx 4{,}585987261
\)

6. Преобразуем десятичную дробь в градусы и минуты. Целая часть — это градусы, а дробную часть умножаем на 60, чтобы получить минуты:
\(
\alpha \approx 4^\circ + 0{,}585987261 \times 60′
\)
\(
\alpha \approx 4^\circ + 35{,}15923566′
\)

7. Округляем минуты до целого числа:
\(
\alpha \approx 4^\circ 35′
\)

Ответ: угол \(\alpha = 4^\circ 35’\).