
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1105 Атанасян — Подробные Ответы
Найдите длину окружности, вписанной: а) в квадрат со стороной a; б) в равнобедренный прямоугольный треугольник с гипотенузой с; в) в прямоугольный треугольник с гипотенузой с и острым углом α; г) в равнобедренный треугольник с углом при основании α и высотой h, проведённой к основанию.
Конечно, без проблем. Вот исправленный текст:
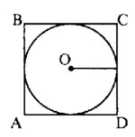
1. а) Дано: \(ABCD\) — квадрат, описанный около окружности \((O; r)\); \(AB = a\). Найти: \(C\).
Решение:
\(
r = \frac{a}{2}
\)
\(
C = 2\pi r = 2\pi \cdot \frac{a}{2} = \pi a
\)
2. б) Дано: \(\triangle ABC\) описан в окружности \((O; r)\); \(AC = BC = b\), \(AB = a\), \(\angle C = 90^\circ\). Найти: \(C\).
Решение:
\(
AC^2 + BC^2 = AB^2 \Rightarrow 2AC^2 = c^2 \Rightarrow AC = \frac{c\sqrt{2}}{2}
\)
\(
AM = BN = \frac{c\sqrt{2}}{2} — r
\)
\(
AB = AE + EB \Rightarrow 0 = 2\left(\frac{c\sqrt{2}}{2} — r\right) = c\sqrt{2} — 2r \Rightarrow r = \frac{c(\sqrt{2} — 1)}{2}
\)
\(
C = 2\pi r = 2\pi \cdot \frac{c(\sqrt{2} — 1)}{2} = \pi c (\sqrt{2} — 1)
\)
3. в) Дано: \(\triangle ABC\) описан около окружности \((O; r)\); \(AB = c\), \(\angle C = 90^\circ\); \(\angle A = \alpha\). Найти: \(C\).
Решение:
\(
BC = c \cdot \sin \alpha, \quad AC = c \cdot \cos \alpha
\)
\(
BC + AB + AC = c \Rightarrow c \cdot \sin \alpha + c + c \cdot \cos \alpha — r = c
\)
\(
c(\sin \alpha + \cos \alpha — 1) = 2r \Rightarrow r = \frac{c(\sin \alpha + \cos \alpha — 1)}{2}
\)
\(
C = 2\pi r = \pi c (\sin \alpha + \cos \alpha — 1)
\)
4. г) Дано: \(\triangle ABC\) описан около окружности \((O; r)\); \(AB = BC\), \(\angle A = \alpha\); \(BH \perp AC\); \(BH = h\). Найти: \(C\).
Решение:
\(
AH = \frac{BH}{\tan \alpha} = \frac{h}{\tan \alpha}
\)
Пусть \(HO = r\), тогда
\(
R = AH \cdot \tan \frac{\alpha}{2} = \frac{h \cdot \tan \frac{\alpha}{2}}{\tan \alpha}
\)
\(
C = 2\pi R = 2\pi \cdot \frac{h \cdot \tan \frac{\alpha}{2}}{\tan \alpha}
\)
Извините за ошибку. Давайте исправим обозначения:
1. Дано: \(ABCD\) — квадрат, описанный около окружности \((O; r)\); \(AB = a\). Найти: \(C\).
Решение:
Радиус окружности, вписанной в квадрат, равен половине стороны квадрата:
\( r = \frac{a}{2} \)
Длина окружности:
\( C = 2\pi r = 2\pi \cdot \frac{a}{2} = \pi a \)
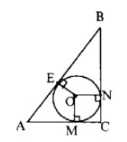
2. Дано: \(\triangle ABC\) описан в окружности \((O; r)\); \(AC = BC = b\), \(AB = a\), \(\angle C = 90^\circ\). Найти: \(C\).
Решение:
В прямоугольном треугольнике:
\( AC^2 + BC^2 = AB^2 \Rightarrow 2AC^2 = c^2 \Rightarrow AC = \frac{c\sqrt{2}}{2} \)
Поскольку \(AM\) и \(BN\) — касательные, то:
\( AM = BN = \frac{c\sqrt{2}}{2} — r \)
Условие:
\( AB = AE + EB \Rightarrow 0 = 2\left(\frac{c\sqrt{2}}{2} — r\right) = c\sqrt{2} — 2r \)
Решая уравнение, находим \(r\):
\( r = \frac{c(\sqrt{2} — 1)}{2} \)
Длина окружности:
\( C = 2\pi r = 2\pi \cdot \frac{c(\sqrt{2} — 1)}{2} = \pi c (\sqrt{2} — 1) \)
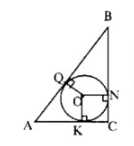
3. Дано: \(\triangle ABC\) описан около окружности \((O; r)\); \(AB = c\), \(\angle C = 90^\circ\); \(\angle A = \alpha\). Найти: \(C\).
Решение:
Выразим стороны треугольника через углы:
\( BC = c \cdot \sin \alpha, \quad AC = c \cdot \cos \alpha \)
Условие:
\( BC + AB + AC = c \Rightarrow c \cdot \sin \alpha + c + c \cdot \cos \alpha — r = c \)
Решая уравнение, находим \(r\):
\( c(\sin \alpha + \cos \alpha — 1) = 2r \Rightarrow r = \frac{c(\sin \alpha + \cos \alpha — 1)}{2} \)
Длина окружности:
\( C = 2\pi r = \pi c (\sin \alpha + \cos \alpha — 1) \)
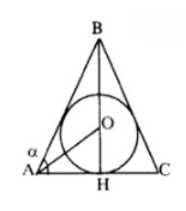
4. Дано: \(\triangle ABC\) описан около окружности \((O; r)\); \(AB = BC\), \(\angle A = \alpha\); \(BH \perp AC\); \(BH = h\). Найти: \(C\).
Решение:
Найдем \(AH\) через \(BH\) и угол \(\alpha\):
\( AH = \frac{BH}{\tan \angle A} = \frac{h}{\tan \alpha} \)
Пусть \(HO = r\), тогда радиус описанной окружности:
\( R = AH \cdot \tan \frac{\alpha}{2} = \frac{h \cdot \tan \frac{\alpha}{2}}{\tan \alpha} \)
Длина окружности:
\( C = 2\pi r = 2\pi \cdot \frac{h \cdot \tan \frac{\alpha}{2}}{\tan \alpha} \)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!