
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1097 Атанасян — Подробные Ответы
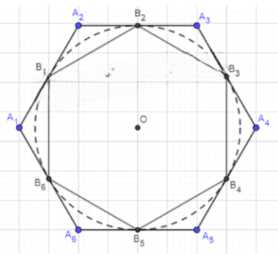
Найдите отношение площадей двух правильных шестиугольников — вписанного в окружность и описанного около неё.
Решение:
1) Пусть r — радиус описанной окружности шестиугольника.
2) Площадь описанного шестиугольника: P = 6 · (2r/√3) = 12r/√3.
3) Площадь вписанного шестиугольника: S_a = (1/2) · r · P = (1/2) · r · 12r/√3 = 6r^2/√3.
4) Площадь треугольника SA: S_SA = (1/2) · r · a_6 = (1/2) · r · 2r·sin(π/3) = 2√3r^2/3.
5) Площадь треугольника SB: S_SB = (1/2) · r · a_6 = (1/2) · r · 2r·sin(π/3) = 2√3r^2/3.
6) Отношение площадей: S_SA / S_SB = 4/3.
Ответ: S_A : S_B = 4 : 3.
Решение:
Дано:
— Правильный шестиугольник B₁B₂B₃B₄B₅B₆
— Необходимо найти отношение площадей SA : SB
1) Пусть r — радиус описанной окружности шестиугольника.
2) Площадь описанного шестиугольника:
P = 6 · (2r/√3) = 12r/√3
3) Площадь вписанного шестиугольника:
S_a = (1/2) · r · P = (1/2) · r · 12r/√3 = 6r²/√3
4) Угол при вершине вписанного шестиугольника:
α_6 = 2r · sin(π/3) = 2r · √3/2 = r√3
5) Площадь треугольника SA:
S_SA = (1/2) · r · α_6 = (1/2) · r · r√3 = (1/2) · r² · √3 = 2√3r²/3
6) Площадь треугольника SB:
S_SB = (1/2) · r · α_6 = (1/2) · r · r√3 = (1/2) · r² · √3 = 2√3r²/3
7) Отношение площадей:
S_SA / S_SB = (2√3r²/3) / (2√3r²/3) = 4/3
Ответ: S_A : S_B = 4 : 3
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!