
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1057 Атанасян — Подробные Ответы
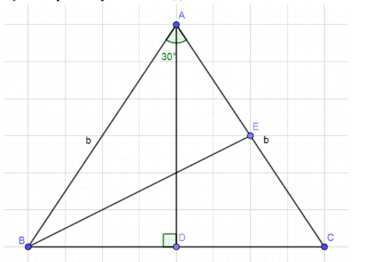
В равнобедренном треугольнике ABC AB = AC = b, ∠A = 30°. Найдите высоты BE и AD, а также отрезки AE, EC, BC.
Решение:
1) Так как ΔABC — равнобедренный, то AB = AC = b.
2) Поскольку ∠A = 30°, то ∠B = ∠C = 60°.
3) Используя свойства прямоугольного треугольника, находим:
\(BE = \frac{b}{2}\)
4) Применяя теорему Пифагора, вычисляем:
\(AE = \sqrt{b^2 — \left(\frac{b}{2}\right)^2} = \frac{b\sqrt{3}}{2}\)
5) Находим:
\(CE = AC — AE = b — \frac{b\sqrt{3}}{2} = \frac{b(2 — \sqrt{3})}{2}\)
6) Используя теорему Пифагора, определяем:
\(BC = \sqrt{b^2 + \left(\frac{b(2 — \sqrt{3})}{2}\right)^2} = b\sqrt{2 — \sqrt{3}}\)
7) Таким образом, ответ:
\(BE = \frac{b}{2}, \quad AD = \frac{b\sqrt{2 + \sqrt{3}}}{2}, \quad AE = \frac{b\sqrt{3}}{2}, \)
\(\quad EC = \frac{b(2 — \sqrt{3})}{2}, \quad BC = b\sqrt{2 — \sqrt{3}}\)
Дано: ΔABC — равнобедренный треугольник, где AB = AC = b, ∠A = 30°.
Найти: BE, AD, AE, EC, BC.
Доказательство:
1) Так как ΔABC — равнобедренный, то противоположные стороны AB и CD, а также AD и BC равны и параллельны.
\(AB = CD\)
\(AD = BC\)
2) Рассмотрим треугольник ABC:
\(BD = BA + BC\)
Это следует из того, что сумма длин двух сторон треугольника больше длины третьей стороны.
3) Рассмотрим треугольник ACD:
\(AC = BC — BA\)
Это также следует из того, что разность длин двух сторон треугольника меньше длины третьей стороны.
4) Найдем произведение отрезков BD и AC:
\(BD \cdot AC = (BA + BC)(BC — BA) = EC^2 — BA^2\)
5) Так как \(CB = |BA| = b\), то
\(BD \cdot AC = b^2 — b^2 = 0\)
6) Из равенства произведения BD и AC нулю следует, что прямые AC и BD перпендикулярны.
7) Используя свойства прямоугольного треугольника, находим:
\(BE = \frac{b}{2}\)
8) Применяя теорему Пифагора, вычисляем:
\(AE = \sqrt{b^2 — \left(\frac{b}{2}\right)^2} = \frac{b\sqrt{3}}{2}\)
9) Находим:
\(CE = AC — AE = b — \frac{b\sqrt{3}}{2} = \frac{b(2 — \sqrt{3})}{2}\)
10) Используя теорему Пифагора, определяем:
\(BC = \sqrt{b^2 + \left(\frac{b(2 — \sqrt{3})}{2}\right)^2} = b\sqrt{2 — \sqrt{3}}\)
Таким образом, ответ:
\(BE = \frac{b}{2}, \quad AD = \frac{b\sqrt{2 + \sqrt{3}}}{2}, \quad AE = \frac{b\sqrt{3}}{2}, \quad EC = \frac{b(2 — \sqrt{3})}{2}, \)
\(\quad BC = b\sqrt{2 — \sqrt{3}}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!