
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1042 Атанасян — Подробные Ответы
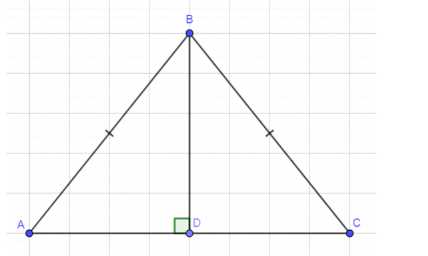
В равностороннем треугольнике АВС со стороной а проведена высота BD. Вычислите скалярное произведение векторов: a) AB · AC; б) AC · CB; в) AC · BD; г) AC · AC.
Решение:
В равностороннем треугольнике ABC со стороной a проведена высота BD. Вычислим скалярные произведения векторов:
a) AB · AC = \(a \cdot a \cdot \cos 60° = a^2 \cdot \frac{1}{2} = \frac{a^2}{2}\)
б) AC · CB = \(a \cdot a \cdot \cos 120° = a^2 \cdot \left(-\frac{1}{2}\right) = -\frac{a^2}{2}\)
в) AC · BD = \(|AC| \cdot |BD| \cdot \cos 90° = a \cdot a \cdot 0 = 0\)
г) AC · AC = \(a \cdot a \cdot \cos 0° = a^2 \cdot 1 = a^2\)
Таким образом, получаем следующие результаты:
a) AB · AC = \(\frac{a^2}{2}\)
б) AC · CB = \(-\frac{a^2}{2}\)
в) AC · BD = 0
г) AC · AC = a^2
Дано: равносторонний треугольник ABC со стороной a, проведена высота BD.
Требуется найти скалярные произведения векторов:
a) AB · AC
б) AC · CB
в) AC · BD
г) AC · AC
Решение:
a) AB · AC
Поскольку треугольник ABC равносторонний, то \(∠A = ∠B = ∠C = 60°\).
Длина вектора AB равна стороне a треугольника.
Длина вектора AC также равна стороне a треугольника.
Угол между векторами AB и AC равен 60°.
Тогда скалярное произведение векторов AB и AC вычисляется по формуле:
\(AB \cdot AC = |AB| \cdot |AC| \cdot \cos 60° = a^2 \cdot \frac{1}{2} = \frac{a^2}{2}\)
б) AC · CB
Угол между векторами AC и CB равен 120°, так как треугольник ABC равносторонний.
Длина вектора AC равна стороне a треугольника.
Длина вектора CB также равна стороне a треугольника.
Скалярное произведение векторов AC и CB вычисляется по формуле:
\(AC \cdot CB = |AC| \cdot |CB| \cdot \cos 120° = a^2 \cdot \left(-\frac{1}{2}\right) = -\frac{a^2}{2}\)
в) AC · BD
Угол между векторами AC и BD равен 90°, так как BD — высота треугольника ABC.
Длина вектора AC равна стороне a треугольника.
Длина вектора BD равна стороне a треугольника.
Скалярное произведение векторов AC и BD вычисляется по формуле:
\(AC \cdot BD = |AC| \cdot |BD| \cdot \cos 90° = a \cdot a \cdot 0 = 0\)
г) AC · AC
Угол между векторами AC и AC равен 0°.
Длина вектора AC равна стороне a треугольника.
Скалярное произведение векторов AC и AC вычисляется по формуле:
\(AC \cdot AC = |AC| \cdot |AC| \cdot \cos 0° = a^2 \cdot 1 = a^2\)
Таким образом, получаем следующие результаты:
a) \(AB \cdot AC = \frac{a^2}{2}\)
б) \(AC \cdot CB = -\frac{a^2}{2}\)
в) \(AC \cdot BD = 0\)
г) \(AC \cdot AC = a^2\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!