ГДЗ по Геометрии 9 класс Номер 1034 Атанасян — Подробные Ответы

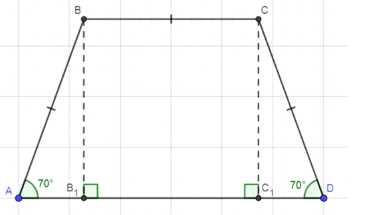
В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно 10 см, а угол при основании равен 70°. Найдите периметр трапеции.

Дано: ABCD — p/6 трапеция; AB = CD = BC; AD = 10 см; ∠AED = 70°. Найти: Площадь трапеции ABCD.

Решение:
1) Пусть AB = x, тогда AB₁ = C₁D = \(\frac{10 — x}{2}\).
2) В △ABB₁: \(\cos 70° = \frac{AB₁}{AB} \Rightarrow 0,342 = \frac{10 — x}{2x} \Rightarrow 0,684x = 10 — x \Rightarrow 1,684x = 10 \Rightarrow \)
\(\Rightarrow x = 5,94 \approx 6 \text{см}\).
3) Площадь трапеции ABCD = AB + BC + CD + AD = 6 · 3 + 10 = 28 см².

Ответ: 28 см².

Дано:
— Трапеция ABCD, где AB = CD = BC и AD = 10 см
— Угол ∠AED = 70°

Решение:
1) Пусть длина AB = x, тогда длина AB₁ = C₁D = (10 — x)/2.
2) В прямоугольном треугольнике ΔAB₁B:
\(\cos 70° = \frac{AB_1}{AB} \Rightarrow 0.342 = \frac{10 — x}{2x} \Rightarrow 0.684x = 10 — x \Rightarrow 1.684x = 10 \Rightarrow \)
\(\Rightarrow x = 5.94 \approx 6 \text{ см}\)
3) Длины сторон трапеции:
— AB = 6 см
— BC = CD = 6 см
— AD = 10 см
4) Площадь трапеции:
\(P_{ABCD} = AB + BC + CD + AD = 6 + 6 + 6 + 10 = 28 \text{ см}^2\)

Ответ: Площадь трапеции PABCD равна 28 см².