
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1023 Атанасян — Подробные Ответы
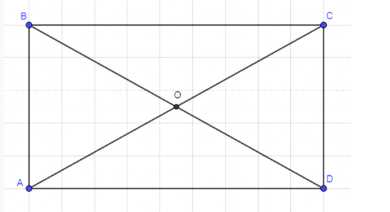
Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями равен 30°.
Решение:
Дано:
— Прямоугольный треугольник ΔABD
— Длина стороны AC = 10 см
— Угол ∠AOB = 30°
Для нахождения площади прямоугольника ABCD:
1. Длина стороны BD = AC = 10 см (по свойству прямоугольника)
2. Длина стороны BO = OD = 5 см (по свойству прямоугольника)
3. Угол ∠COD = ∠AOB = 30° (как вертикальные)
4. Угол ∠BOC = ∠AOD = 150° (как смежные с углом ∠AOB)
5. \( \sin 30° = \sin 150° = \frac{1}{2} \)
Площадь треугольника ΔAOB:
\( S_{AOB} = \frac{1}{2} \cdot AO \cdot BO \cdot \sin \angle AOB = \frac{1}{2} \cdot 5 \cdot 5 \cdot \frac{1}{2} = \frac{25}{4} = 6,25 \text{ см}^2 \)
Площадь треугольника ΔCOD:
\( S_{COD} = \frac{1}{2} \cdot CO \cdot OD \cdot \sin \angle COD = \frac{1}{2} \cdot 5 \cdot 5 \cdot \frac{1}{2} = \frac{25}{4} = 6,25 \text{ см}^2 \)
Площадь треугольника ΔBOC:
\( S_{BOC} = \frac{1}{2} \cdot BO \cdot OC \cdot \sin \angle BOC = \frac{1}{2} \cdot 5 \cdot 5 \cdot \frac{1}{2} = \frac{25}{4} = 6,25 \text{ см}^2 \)
Площадь треугольника ΔAOD:
\( S_{AOD} = \frac{1}{2} \cdot AO \cdot OD \cdot \sin \angle AOD = \frac{1}{2} \cdot 5 \cdot 5 \cdot \frac{1}{2} = \frac{25}{4} = 6,25 \text{ см}^2 \)
Общая площадь прямоугольника ABCD:
\( S_{ABCD} = 4 \cdot \frac{25}{4} = 25 \text{ см}^2 \)
Ответ: 25 см².
Полное решение задачи:
Дано:
— Площадь параллелограмма ΔABC: S_ABC = 60 см²
— Длина стороны AC: AC = 15 см
— Угол между сторонами AB и AD: ∠A = 30°
Требуется найти длину стороны AB.
Решение:
1. Площадь параллелограмма ΔABC можно выразить через длины двух смежных сторон и синус угла между ними:
\( S_{ABC} = \frac{1}{2} \cdot AB \cdot AC \cdot \sin 30^\circ \)
2. Подставим известные значения:
\( 60 = \frac{1}{2} \cdot AB \cdot 15 \cdot \frac{1}{2} \)
3. Упростим уравнение:
\( 60 = \frac{15}{4} \cdot AB \)
4. Найдем длину стороны AB:
\( AB = \frac{60 \cdot 4}{15} = \frac{240}{15} = 16 \)
Ответ: Длина стороны AB равна 16 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!