
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 737 Атанасян — Подробные Ответы
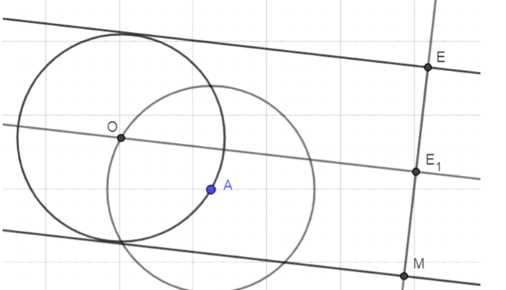
Даны две параллельные прямые и точка, не лежащая ни на одной из них. Постройте окружность, проходящую через данную точку и касающуюся данных прямых.
Для построения окружности, проходящей через точку \( A \) и касающейся данных прямых, выполните следующие шаги:
1. Постройте перпендикуляры к данным прямым через точку \( A \), найдите точки пересечения \( E \) и \( M \) этих перпендикуляров с прямыми.
2. Найдите середину отрезка \( EM \) и постройте серединный перпендикуляр к этому отрезку. Отметьте точку пересечения серединного перпендикуляра с отрезком \( EM \), обозначим её как \( E_1 \).
3. Постройте окружность с центром в точке \( A \) и радиусом, равным расстоянию \( AE_1 \). Найдите точку \( O \) — одну из точек пересечения этой окружности с серединным перпендикуляром.
4. Постройте окружность с центром в точке \( O \) и радиусом, равным расстоянию \( OE_1 \). Это искомая окружность.
Решение задачи о построении окружности, проходящей через точку \( A \) и касающейся данных прямых, выполняется следующим образом:
1. Проведем перпендикуляры к данным прямым через точку \( A \). Пусть прямые обозначены как \( l_1 \) и \( l_2 \). Перпендикуляры пересекут прямые в точках \( E \) и \( M \), соответственно. Точки \( E \) и \( M \) — это основания перпендикуляров, проведенных через точку \( A \) к данным прямым.
2. Найдем середину отрезка \( EM \). Для этого определим координаты точек \( E \) и \( M \) (если задача решается аналитически) или найдем середину отрезка геометрически. Середина отрезка \( EM \) обозначается как точка \( S \). Через точку \( S \) проведем серединный перпендикуляр к отрезку \( EM \).
3. Отметим точку пересечения серединного перпендикуляра с отрезком \( EM \). Пусть эта точка пересечения называется \( E_1 \).
4. Построим окружность с центром в точке \( A \) и радиусом, равным расстоянию \( AE_1 \). Радиус окружности вычисляется как длина отрезка \( AE_1 \), где \( AE_1 \) — расстояние от точки \( A \) до \( E_1 \).
5. Найдем одну из точек пересечения этой окружности с серединным перпендикуляром. Пусть точка пересечения называется \( O \). Точка \( O \) будет центром искомой окружности.
6. Построим окружность с центром в точке \( O \) и радиусом, равным расстоянию \( OE_1 \). Радиус окружности вычисляется как длина отрезка \( OE_1 \), где \( OE_1 \) — расстояние от точки \( O \) до \( E_1 \).
Искомая окружность — это окружность с центром \( O \) и радиусом \( OE_1 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!