ГДЗ по Геометрии 8 класс Номер 736 Атанасян — Подробные Ответы

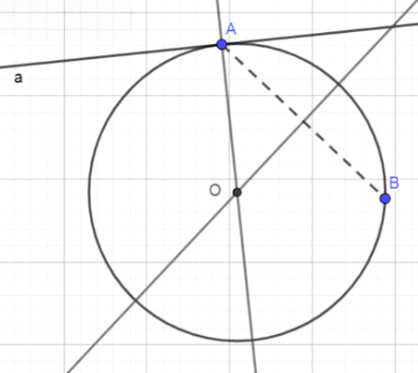
Даны прямая \( a \), точка \( A \), лежащая на этой прямой, и точка \( B \), не лежащая на ней. Постройте окружность, проходящую через точку \( B \) и касающуюся прямой \( a \) в точке \( A \).

Построить окружность, проходящую через точку \( B \) и касающуюся прямой \( a \) в точке \( A \), можно следующим образом:

1. Построим серединный перпендикуляр к отрезку \( AB \).
2. Построим перпендикуляр к прямой \( a \) в точке \( A \).
3. Найдем точку пересечения этих перпендикуляров — это будет центр окружности \( O \).
4. Радиус окружности равен расстоянию \( OA \).
5. Построим окружность с центром \( O \) и радиусом \( OA \).

Искомая окружность готова.

Для построения окружности, проходящей через точку \( B \) и касающейся прямой \( a \) в точке \( A \), выполните следующие шаги:

1. Построим серединный перпендикуляр к отрезку \( AB \).
Серединный перпендикуляр — это прямая, проходящая через середину отрезка \( AB \) и перпендикулярная ему.
Для этого:
— Найдите середину отрезка \( AB \), обозначим её как точку \( M \).
Если координаты точки \( A \) — \( (x_1, y_1) \), а точки \( B \) — \( (x_2, y_2) \), то координаты точки \( M \) вычисляются по формуле:
\[
M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)
\]
— Постройте прямую через точку \( M \), перпендикулярную отрезку \( AB \). Для этого определите угловой коэффициент прямой \( AB \):
\[
k_{AB} = \frac{y_2 — y_1}{x_2 — x_1}
\]
Угловой коэффициент серединного перпендикуляра будет равен \( k = -\frac{1}{k_{AB}} \).

2. Построим перпендикуляр к прямой \( a \) в точке \( A \).
Прямая \( a \) задана уравнением, например, \( y = k_a x + b \).
— Угловой коэффициент перпендикуляра к прямой \( a \) будет равен \( k = -\frac{1}{k_a} \).
— Постройте прямую через точку \( A \) с этим угловым коэффициентом.

3. Найдем точку пересечения этих двух перпендикуляров.
Пересечение двух прямых можно найти, решив их систему уравнений. Пусть уравнение серединного перпендикуляра имеет вид:
\[
y = k_1 x + b_1
\]
А уравнение перпендикуляра к прямой \( a \):
\[
y = k_2 x + b_2
\]
Решив систему:
\[
\begin{cases}
y = k_1 x + b_1 \\
y = k_2 x + b_2
\end{cases}
\]
Найдем координаты точки пересечения \( O(x_O, y_O) \).

4. Радиус окружности равен расстоянию \( OA \).
Расстояние между точками \( O(x_O, y_O) \) и \( A(x_1, y_1) \) вычисляется по формуле:
\[
OA = \sqrt{(x_O — x_1)^2 + (y_O — y_1)^2}
\]

5. Построим окружность с центром в точке \( O \) и радиусом \( OA \).
Уравнение окружности будет иметь вид:
\[
(x — x_O)^2 + (y — y_O)^2 = OA^2
\]
Это искомая окружность.

Таким образом, окружность построена.