ГДЗ по Геометрии 8 класс Номер 735 Атанасян — Подробные Ответы

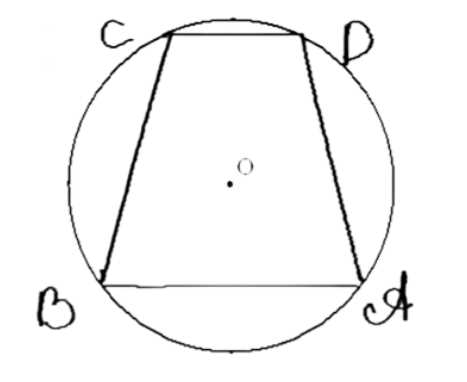
В трапецию с основаниями \( a \) и \( b \) можно вписать окружность и около этой трапеции можно описать окружность. Найдите радиус вписанной окружности.

Дано: \(ABCD\) — трапеция, \(AD = a\), \(BC = b\). Найти \(r\).

Решение:
Так как \(ABCD\) — равнобедренная трапеция, вписанная в окружность, то \(AB = CD\).
Из свойства описанной трапеции:
\(
AB + CD = AD + BC = a + b,
\)
отсюда:
\(
AB = \frac{a + b}{2}.
\)
Высота трапеции равна \(BE = CF\). Рассмотрим прямоугольный треугольник \(ABE\):
\(
BE^2 = AB^2 — AE^2.
\)
Подставим значения:
\(
AE = \frac{a — b}{2}, \quad AB = \frac{a + b}{2}.
\)
Тогда:
\(
BE^2 = \left(\frac{a + b}{2}\right)^2 — \left(\frac{a — b}{2}\right)^2 = ab.
\)
Следовательно:
\(
BE = \sqrt{ab}.
\)
Так как \(BE = 2r\), то:
\(
r = \frac{\sqrt{ab}}{2}.
\)

Ответ:
\(
r = \frac{\sqrt{ab}}{2}.
\)

Дано: \(ABCD\) — трапеция, \(AD = a\), \(BC = b\). Найти радиус \(r\) вписанной окружности.

Решение:
1. Трапеция \(ABCD\) вписана в окружность, поэтому она является равнобедренной. Следовательно, \(AB = CD\).

2. Трапеция \(ABCD\) описана около окружности, значит, сумма длин противоположных сторон равна:
\(
AB + CD = AD + BC = a + b.
\)
Так как \(AB = CD\), то:
\(
AB = CD = \frac{a + b}{2}.
\)

3. Проведем высоты \(BE\) и \(CF\), которые являются перпендикулярами к основаниям \(AD\) и \(BC\).

4. Рассмотрим прямоугольный треугольник \(ABE\). В нем гипотенуза \(AB = \frac{a + b}{2}\), а один из катетов \(AE = \frac{a — b}{2}\) (разность оснований трапеции делится поровну между двумя равными боковыми сторонами).

По теореме Пифагора запишем:
\(
BE^2 = AB^2 — AE^2.
\)
Подставим значения \(AB\) и \(AE\):
\(
BE^2 = \left(\frac{a + b}{2}\right)^2 — \left(\frac{a — b}{2}\right)^2.
\)

Раскроем скобки:
\(
BE^2 = \frac{(a + b)^2}{4} — \frac{(a — b)^2}{4}.
\)

Выполним вычисления:
\(
BE^2 = \frac{a^2 + 2ab + b^2}{4} — \frac{a^2 — 2ab + b^2}{4}.
\)

Сократим подобные члены:
\(
BE^2 = \frac{a^2 + 2ab + b^2 — a^2 + 2ab — b^2}{4}.
\)

Получаем:
\(
BE^2 = \frac{4ab}{4}.
\)

Итак:
\(
BE^2 = ab.
\)

Следовательно:
\(
BE = \sqrt{ab}.
\)

5. Радиус вписанной окружности равен половине высоты трапеции, то есть:
\(
r = \frac{BE}{2}.
\)

Подставим значение \(BE\):
\(
r = \frac{\sqrt{ab}}{2}.
\)

Ответ:
\(
r = \frac{\sqrt{ab}}{2}.
\)