Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 730 Атанасян — Подробные Ответы
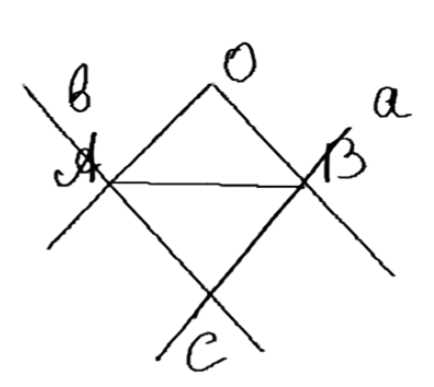
Через точки \( A \) и \( B \) проведены прямые, перпендикулярные к сторонам угла \( AOB \) и пересекающиеся в точке \( C \) внутри угла. Докажите, что около четырёхугольника \( ACBO \) можно описать окружность.
Доказать, что если сумма противоположных углов четырёхугольника равна \(180^\circ\), то около него можно описать окружность.
Пусть четырёхугольник \(ABCD\) такой, что \(\angle A + \angle C = 180^\circ\). Проведём окружность через вершины \(A, B\) и \(D\) и докажем, что она проходит через вершину \(C\).
Предположим, что вершина \(C\) не лежит на окружности. Тогда она либо внутри круга, либо вне его:
1) Если \(C\) внутри круга, то \(\angle C = \frac{1}{2} (\angle DAB + \angle EF)\), а значит, \(\angle C > \angle DAB\). Учитывая, что \(\angle A = \frac{1}{2} \angle BD\), получаем \(\angle A + \angle C > \frac{1}{2} (\angle BED + \angle DAB) = \frac{1}{2} \cdot 360^\circ = 180^\circ\), что противоречит условию.
2) Аналогично для случая, если \(C\) вне круга.
Следовательно, вершина \(C\) лежит на окружности, и вокруг четырёхугольника \(ABCD\) можно описать окружность.
Дано:
\[
\angle AOB; \quad AC \perp AO; \quad BC \perp BO; \quad AC \cap BC = C;
\]
Доказать: около \(ACBO\) можно описать окружность.
Решение:
1. По условию \(AC \perp AO\) и \(BC \perp BO\), следовательно, углы \(OAC\) и \(OBC\) прямые:
\[
\angle OAC = 90^\circ \quad \text{и} \quad \angle OBC = 90^\circ.
\]
2. В любом четырёхугольнике сумма углов равна \(360^\circ\) (по теореме о сумме углов в многоугольнике):
\[
\angle A + \angle B + \angle C + \angle O = 360^\circ.
\]
Из условия известно, что \(AC \perp AO\) и \(BC \perp BO\), поэтому
\[
\angle A = 90^\circ \quad \text{и} \quad \angle B = 90^\circ.
\]
Подставляем значения углов \(A\) и \(B\) в формулу:
\[
90^\circ + 90^\circ + \angle C + \angle O = 360^\circ.
\]
Упростим выражение:
\[
\angle C + \angle O = 360^\circ — (90^\circ + 90^\circ) = 180^\circ.
\]
3. В выпуклом четырёхугольнике, если сумма противоположных углов равна \(180^\circ\), то около него можно описать окружность. В данном случае:
\[
\angle A + \angle B = 180^\circ \quad \text{и} \quad \angle O + \angle C = 180^\circ.
\]
Следовательно, около четырёхугольника \(ACBO\) можно описать окружность, что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.