Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 729 Атанасян — Подробные Ответы
Докажите, что если в четырёхугольнике сумма противоположных углов равна \(180^\circ\), то около этого четырёхугольника можно описать окружность.
Решение
Пусть в четырёхугольнике \(ABCD\)
\[
\angle A + \angle C = 180^\circ.
\]
(1)
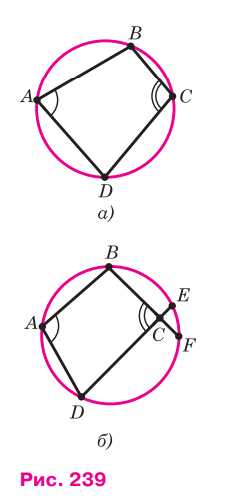
Проведём окружность через три вершины четырёхугольника: \(A, B\) и \(D\) (рис. 239, а) — и докажем, что она проходит также через вершину \(C\), т.е. является описанной около четырёхугольника \(ABCD\). Предположим, что это не так. Тогда вершина \(C\) лежит либо внутри круга, либо вне его. Рассмотрим первый случай (рис. 239, б). В этом случае
\[
\angle C = \frac{1}{2} (\overset{\frown}{DAB} + \overset{\frown}{EF}),
\]
(см. задачу 718), и, следовательно,
\[
\angle C > \frac{1}{2} \overset{\frown}{DAB}.
\]
Так как
\[
\angle A = \frac{1}{2} \overset{\frown}{BED},
\]
то
\[
\angle A + \angle C > \frac{1}{2} (\overset{\frown}{BED} + \overset{\frown}{DAB}) = \frac{1}{2} \cdot 360^\circ = 180^\circ.
\]
Итак, мы получили, что \(\angle A + \angle C > 180^\circ\). Но это противоречит условию (1), и, значит, наше предположение ошибочно. Аналогично можно доказать (опираясь на задачу 719), что вершина \(C\) не может лежать вне круга. Следовательно, вершина \(C\) лежит на окружности, что и требовалось доказать.
Доказать, что если сумма противоположных углов четырёхугольника равна \(180^\circ\), то около него можно описать окружность.
Пусть четырёхугольник \(ABCD\) такой, что \(\angle A + \angle C = 180^\circ\). Проведём окружность через вершины \(A, B\) и \(D\) и докажем, что она проходит через вершину \(C\).
Предположим, что вершина \(C\) не лежит на окружности. Тогда она либо внутри круга, либо вне его:
1) Если \(C\) внутри круга, то \(\angle C = \frac{1}{2} (\angle DAB + \angle EF)\), а значит, \(\angle C > \angle DAB\). Учитывая, что \(\angle A = \frac{1}{2} \angle BD\), получаем \(\angle A + \angle C > \frac{1}{2} (\angle BED + \angle DAB) = \frac{1}{2} \cdot 360^\circ = 180^\circ\), что противоречит условию.
2) Аналогично для случая, если \(C\) вне круга.
Следовательно, вершина \(C\) лежит на окружности, и вокруг четырёхугольника \(ABCD\) можно описать окружность.
Доказать: Если в четырёхугольнике сумма противоположных углов равна \(180^\circ\), то около него можно описать окружность.
Доказательство:
Пусть \(ABCD\) — четырёхугольник, для которого выполняется условие:
\[
\angle A + \angle C = 180^\circ.
\]
1. Проведём окружность через три вершины четырёхугольника \(A, B\) и \(D\). Нам нужно доказать, что эта окружность проходит также через вершину \(C\).
2. Предположим противное: вершина \(C\) не лежит на окружности. Тогда она может находиться либо внутри окружности, либо вне её.
3. Рассмотрим первый случай, когда вершина \(C\) находится внутри окружности. В этом случае угол \(\angle C\) можно выразить через дуги окружности следующим образом:
\[
\angle C = \frac{1}{2} (\overset{\frown}{DAB} + \overset{\frown}{EF}),
\]
где \(\overset{\frown}{DAB}\) — дуга окружности, соответствующая углу \(\angle DAB\), а \(\overset{\frown}{EF}\) — дополнительная дуга, возникающая из-за положения вершины \(C\) внутри круга.
Так как \(\angle C = \frac{1}{2} (\overset{\frown}{DAB} + \overset{\frown}{EF})\), то очевидно, что
\[
\angle C > \frac{1}{2} \overset{\frown}{DAB}.
\]
Угол \(\angle A\) выражается через ту же дугу \(\overset{\frown}{DAB}\):
\[
\angle A = \frac{1}{2} \overset{\frown}{BD}.
\]
Тогда сумма углов \(\angle A + \angle C\) будет равна:
\[
\angle A + \angle C > \frac{1}{2} (\overset{\frown}{BD} + \overset{\frown}{BED}).
\]
Но \(\overset{\frown}{BD} + \overset{\frown}{BED} = 360^\circ\), поэтому:
\[
\angle A + \angle C > \frac{1}{2} \cdot 360^\circ = 180^\circ.
\]
Это противоречит исходному условию задачи, согласно которому \(\angle A + \angle C = 180^\circ\).
4. Аналогично рассматривается случай, когда вершина \(C\) находится вне окружности. В этом случае угол \(\angle C\) выражается как разность дуг:
\[
\angle C = \frac{1}{2} (\overset{\frown}{DAB} — \overset{\frown}{EF}),
\]
и аналогичным образом получается противоречие с условием задачи.
5. Таким образом, наше предположение о том, что вершина \(C\) не лежит на окружности, оказалось неверным.
6. Следовательно, вершина \(C\) лежит на окружности. Это означает, что около четырёхугольника \(ABCD\) можно описать окружность, что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.