
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 728 Атанасян — Подробные Ответы
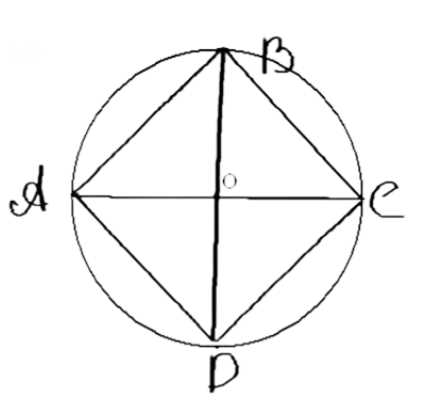
Докажите, что если около ромба можно описать окружность, то этот ромб — квадрат.
Дано: \( ABCD \) — ромб вписанный.
Доказательство:
По свойству описанной окружности около четырёхугольника:
\( \angle A + \angle C = \angle B + \angle D = 180^\circ \).
По свойству ромба:
\( \angle A = \angle C \), \( \angle B = \angle D \).
Следовательно:
\( \angle A = \angle B = \angle C = \angle D = 90^\circ \).
Таким образом, \( ABCD \) — квадрат.
Дано: \( ABCD \) — ромб вписанный.
Доказать: \( ABCD \) — квадрат.
Решение:
1. Вписанный ромб \( ABCD \) имеет описанную окружность. По свойству описанной окружности около четырёхугольника сумма противоположных углов равна \( 180^\circ \):
\( \angle A + \angle C = \angle B + \angle D = 180^\circ. \)
2. По свойству ромба противоположные углы равны:
\( \angle A = \angle C, \quad \angle B = \angle D. \)
3. Подставим равенства углов в уравнение:
\( 2 \angle A = 180^\circ, \quad 2 \angle B = 180^\circ. \)
4. Найдём значения углов:
\( \angle A = \angle B = \angle C = \angle D = 90^\circ. \)
5. Таким образом, ромб \( ABCD \) имеет все углы равные \( 90^\circ \), а значит, он является квадратом.
Ответ: \( ABCD \) — квадрат.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!