ГДЗ по Геометрии 8 класс Номер 726 Атанасян — Подробные Ответы

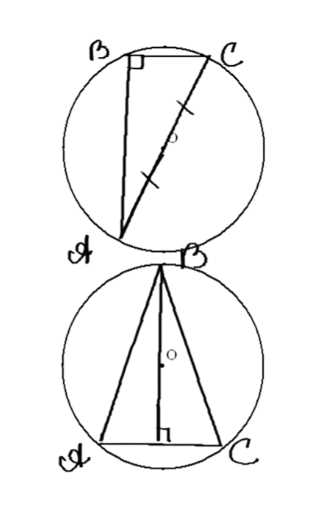
Центр описанной около треугольника окружности лежит на медиане. Докажите, что этот треугольник либо равнобедренный, либо прямоугольный.

дано: \( \Delta ABC \) — вписанный; \( \text{Окр } (O; r) \); \( O \in \text{медиане} \).

доказать: \( \Delta ABC \) — \( \pi/6 \) или прямоугольный.

решение:
1. Центр окружности \( O \) лежит на медиане \( BD \), которая одновременно является серединным перпендикуляром. Следовательно, углы \( \angle ADB \) и \( \angle CDB \) равны \( 90^\circ \).
2. Треугольники \( \Delta ABD \) и \( \Delta BCD \) прямоугольные, имеют общий катет \( BD \) и равные гипотенузы (\( AD = DC \)). Значит, \( AB = BC \), и треугольник \( \Delta ABC \) равнобедренный.
3. Так как медиана \( CO \) совпадает с диаметром окружности, угол \( \angle ACB \) опирается на диаметр и равен \( 90^\circ \).

Таким образом, \( \Delta ABC \) — прямоугольный, что и требовалось доказать.

Дано: \( \Delta ABC \) — вписанный, центр описанной окружности \( O \) лежит на медиане \( BD \).

Требуется доказать: \( \Delta ABC \) либо прямоугольный, либо один из его углов равен \( \pi/6 \).

Решение:

1. Так как треугольник \( \Delta ABC \) вписан в окружность, то центр описанной окружности \( O \) является точкой пересечения серединных перпендикуляров к сторонам треугольника.

2. По условию центр окружности \( O \) лежит на медиане \( BD \). Медиана \( BD \) делит сторону \( AC \) пополам, то есть \( AD = DC \).

3. Центр окружности \( O \), лежащий на медиане \( BD \), также находится на равном расстоянии от всех вершин треугольника. Это возможно только в одном из двух случаев:
а) медиана \( BD \) является высотой, то есть угол \( \angle ADB = \angle CDB = 90^\circ \);
б) треугольник \( \Delta ABC \) равнобедренный с углом при вершине \( B \), равным \( \pi/3 \), что делает углы при основании \( \pi/6 \).

4. Рассмотрим первый случай: если медиана \( BD \) является также высотой, то треугольник \( \Delta ABC \) прямоугольный. Угол \( \angle ACB \), опирающийся на диаметр описанной окружности, равен \( 90^\circ \).

5. Рассмотрим второй случай: если \( \Delta ABC \) равнобедренный и угол при вершине \( B \) равен \( \pi/3 \), то углы при основании \( A \) и \( C \) равны \( \pi/6 \). Это следует из свойства углов равнобедренного треугольника, сумма которых равна \( \pi \).

Вывод: треугольник \( \Delta ABC \) либо прямоугольный, либо один из его углов равен \( \pi/6 \).