ГДЗ по Геометрии 8 класс Номер 724 Атанасян — Подробные Ответы

Докажите, что если в выпуклом четырёхугольнике суммы противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

Решение:

Пусть в выпуклом четырёхугольнике \(ABCD\):
\[
AB + CD = BC + AD.
\]
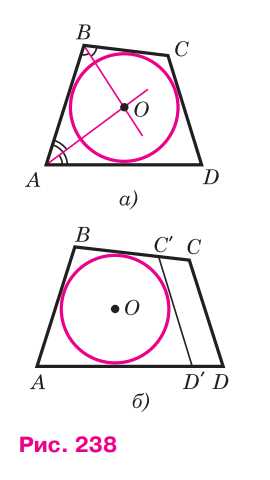
Точка \(O\) пересечения биссектрис углов \(A\) и \(B\) равноудалена от сторон \(AD\), \(AB\) и \(BC\), поэтому можно провести окружность с центром \(O\), касающуюся указанных трёх сторон (рис. 238, а). Докажем, что эта окружность касается также стороны \(CD\) и, значит, является вписанной в четырёхугольник \(ABCD\).

Предположим, что это не так. Тогда прямая \(CD\) либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (рис. 238, б). Проведём касательную \(C’D’\), параллельную стороне \(CD\) (\(C’\) и \(D’\) — точки пересечения касательной со сторонами \(BC\) и \(AD\)). Так как \(ABC’D’\) — описанный четырёхугольник, то по свойству его сторон:
\[
AB + C’D’ = BC’ + AD’.
\]
Но \(BC’ = BC — C’C\), \(AD’ = AD — D’D\), поэтому из равенства получаем:
\[
C’D’ + C’C + D’D = BC + AD — AB.
\]
Правая часть этого равенства в силу условия равна \(CD\). Таким образом, приходим к равенству:
\[
C’D’ + C’C + D’D = CD,
\]
то есть в четырёхугольнике \(C’CDD’\) одна сторона равна сумме трёх других сторон. Но этого не может быть, и, значит, наше предположение ошибочно. Аналогично можно доказать, что прямая \(CD\) не может быть секущей окружности. Следовательно, окружность касается стороны \(CD\), что и требовалось доказать.

Решение:

Пусть в выпуклом четырехугольнике \(ABCD\):
\[
AB + CD = BC + AD.
\]

Точка \(O\), пересечение биссектрис углов \(A\) и \(B\), равноудалена от сторон \(AB\), \(AD\) и \(BC\). Значит, окружность можно вписать, касаясь этих трех сторон.

Предположим, что окружность не касается стороны \(CD\). Тогда \(CD\) либо не имеет общих точек с окружностью, либо является секущей.

Если \(CD\) не имеет общих точек, проведем касательную \(C’D’\), параллельную \(CD\). Для четырехугольника \(ABC’D’\) выполняется:
\[
AB + C’D’ = BC’ + AD’,
\]
где \(BC’ = BC — C’C\), \(AD’ = AD — D’D\). Тогда:
\[
C’D’ + C’C + D’D = BC + AD — AB.
\]

Получается:
\[
C’D’ + C’C + D’D = CD,
\]
то есть одна сторона четырехугольника равна сумме других, что противоречит условию.

Аналогично доказывается, что \(CD\) не может быть секущей. Следовательно, \(CD\) — касательная, и окружность вписана в четырехугольник.

Решение:

Пусть дан выпуклый четырехугольник \(ABCD\), для которого выполняется условие:
\[
AB + CD = BC + AD.
\]
Необходимо доказать, что в этот четырехугольник можно вписать окружность.

1. Рассмотрим точку \(O\), которая является точкой пересечения биссектрис углов \(A\) и \(B\). Из свойства биссектрис известно, что точка \(O\) равноудалена от сторон \(AB\), \(AD\) и \(BC\). Это означает, что можно вписать окружность, касающуюся этих трех сторон.

2. Далее необходимо доказать, что эта окружность также касается стороны \(CD\). Предположим, что окружность не касается стороны \(CD\). Тогда возможны два случая:
— \(CD\) не имеет общих точек с окружностью;
— \(CD\) является секущей.

3. Рассмотрим первый случай, когда \(CD\) не имеет общих точек с окружностью. В этом случае проведем касательную \(C’D’\), параллельную \(CD\), так чтобы окружность касалась сторон \(AB\), \(BC\), \(AD\) и \(C’D’\). Тогда четырехугольник \(ABC’D’\) будет описанным, и для его сторон выполняется равенство:
\[
AB + C’D’ = BC’ + AD’,
\]
где \(BC’ = BC — C’C\) и \(AD’ = AD — D’D\). Подставим эти выражения в равенство:
\[
AB + C’D’ = (BC — C’C) + (AD — D’D).
\]
Перенесем \(AB\) в правую часть:
\[
C’D’ + C’C + D’D = BC + AD — AB.
\]
Заметим, что \(BC + AD — AB = CD\) по условию задачи. Следовательно:
\[
C’D’ + C’C + D’D = CD.
\]
Это противоречит предположению, что \(CD\) не имеет общих точек с окружностью, так как сторона \(CD\) оказывается равной сумме других сторон.

4. Рассмотрим второй случай, когда \(CD\) является секущей. Аналогично предыдущему рассуждению можно показать, что это приводит к противоречию, так как в этом случае одна из сторон четырехугольника окажется равной сумме других сторон, что невозможно для выпуклого четырехугольника.

5. Таким образом, оба предположения о том, что \(CD\) либо не имеет общих точек с окружностью, либо является секущей, приводят к противоречию. Следовательно, сторона \(CD\) является касательной к окружности.

6. Из доказанного следует, что окружность касается всех четырех сторон четырехугольника \(ABCD\), то есть окружность вписана в данный четырехугольник.

Ответ: окружность вписана в четырехугольник \(ABCD\).