
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 722 Атанасян — Подробные Ответы
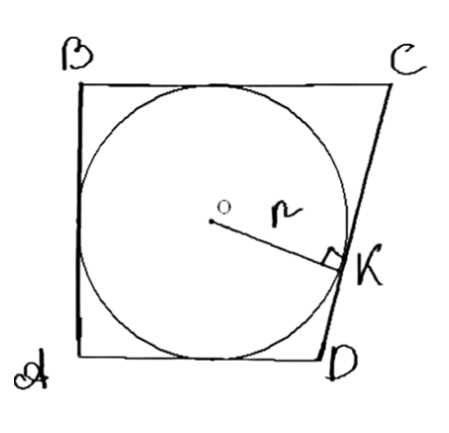
Четырёхугольник \(ABCD\) описан около окружности радиуса \(r\). Известно, что \(AB : CD = 2 : 3\), \(AD : BC = 2 : 1\). Найдите стороны четырёхугольника, если его площадь равна \(S\).
Дано: \(AB : CD = 2 : 3\), \(AD : BC = 2 : 1\), \(\text{S}_{ABCD} = S\). Вписанная окружность радиуса \(r\).
Решение:
1) Радиус окружности:
\(
r = \frac{2S}{P_{ABCD}}, \quad \text{где} \quad P = \frac{2S}{r}.
\)
2) По свойству вписанной окружности:
\(
AB + CD = BC + AD = \frac{S}{r}.
\)
3) Пусть \(AB = 2x\), \(CD = 3x\):
\(
2x + 3x = \frac{S}{r}, \quad \text{отсюда} \quad x = \frac{S}{5r}, \quad AB = \frac{2S}{5r}, \quad CD = \frac{3S}{5r}.
\)
4) Пусть \(AD = 2y\), \(BC = y\):
\(
2y + y = \frac{S}{r}, \quad \text{отсюда} \quad y = \frac{S}{3r}, \quad BC = \frac{S}{3r}, \quad AD = \frac{2S}{3r}.
\)
Ответ:
\(
AB = \frac{2S}{5r}, \quad CD = \frac{3S}{5r}, \quad BC = \frac{S}{3r}, \quad AD = \frac{2S}{3r}.
\)
Все дробные ответы уже представлены в виде несократимых дробей.
Дано: четырехугольник \(ABCD\) с вписанной окружностью, радиус которой равен \(r\). Известно, что отношения сторон \(AB : CD = 2 : 3\) и \(AD : BC = 2 : 1\). Площадь четырехугольника равна \(S\). Требуется найти длины сторон \(AB\), \(BC\), \(CD\), \(AD\).
Решение:
1) Вписанная окружность существует в четырехугольнике, если сумма длин противоположных сторон равна:
\(
AB + CD = AD + BC.
\)
2) Периметр четырехугольника выражается через радиус окружности и площадь:
\(
P = \frac{2S}{r}.
\)
3) Так как \(AB + CD = AD + BC\), то каждая из этих сумм равна половине периметра:
\(
AB + CD = AD + BC = \frac{P}{2}.
\)
4) Подставим значение периметра:
\(
AB + CD = AD + BC = \frac{S}{r}.
\)
5) Пусть \(AB = 2x\) и \(CD = 3x\) (по условию \(AB : CD = 2 : 3\)). Тогда:
\(
AB + CD = 2x + 3x = 5x.
\)
6) Из условия \(AB + CD = \frac{S}{r}\) получаем:
\(
5x = \frac{S}{r}, \quad x = \frac{S}{5r}.
\)
Теперь найдем \(AB\) и \(CD\):
\(
AB = 2x = 2 \cdot \frac{S}{5r} = \frac{2S}{5r},
\)
\(
CD = 3x = 3 \cdot \frac{S}{5r} = \frac{3S}{5r}.
\)
7) Пусть \(AD = 2y\) и \(BC = y\) (по условию \(AD : BC = 2 : 1\)). Тогда:
\(
AD + BC = 2y + y = 3y.
\)
8) Из условия \(AD + BC = \frac{S}{r}\) получаем:
\(
3y = \frac{S}{r}, \quad y = \frac{S}{3r}.
\)
Теперь найдем \(AD\) и \(BC\):
\(
AD = 2y = 2 \cdot \frac{S}{3r} = \frac{2S}{3r},
\)
\(
BC = y = \frac{S}{3r}.
\)
Ответ:
\(
AB = \frac{2S}{5r}, \quad CD = \frac{3S}{5r}, \quad BC = \frac{S}{3r}, \quad AD = \frac{2S}{3r}.
\)
Все дроби являются несократимыми, и их нельзя представить в виде смешанных чисел.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!