ГДЗ по Геометрии 8 класс Номер 719 Атанасян — Подробные Ответы

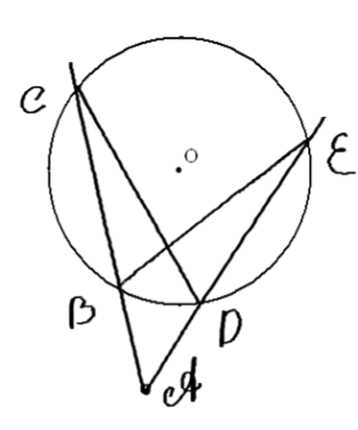
Через точку, лежащую вне окружности, проведены две секущие. Докажите, что угол между ними измеряется полуразностью дуг, заключённых внутри угла.

Дано: окружность \((O; r)\), \(AC\), \(AE\) — секущие.

Доказать:
\(
\angle CAE = \frac{1}{2} (\overset{\frown}{CE} — \overset{\frown}{BD}).
\)

Рассмотрим треугольник \(\triangle ACD\). По теореме о сумме углов треугольника:
\(
\angle A = 180^\circ — (\angle C + \angle D).
\)
Угол \(\angle D\) является смежным с \(\angle CDE\), поэтому:
\(
\angle D = 180^\circ — \angle CDE.
\)
Угол \(\angle CDE\) — вписанный, следовательно:
\(
\angle CDE = \frac{1}{2} \overset{\frown}{CE}.
\)
Подставим:
\(
\angle D = 180^\circ — \frac{1}{2} \overset{\frown}{CE}.
\)
Угол \(\angle C\) также вписанный, поэтому:
\(
\angle C = \frac{1}{2} \overset{\frown}{BD}.
\)
Теперь выразим угол \(\angle CAE\):
\(
\angle CAE = 180^\circ — (\angle C + \angle D).
\)
Подставим значения:
\(
\angle CAE = 180^\circ — \left(\frac{1}{2} \overset{\frown}{BD} + \left(180^\circ — \frac{1}{2} \overset{\frown}{CE}\right)\right).
\)
Раскроем скобки:
\(
\angle CAE = 180^\circ — \frac{1}{2} \overset{\frown}{BD} — 180^\circ + \frac{1}{2} \overset{\frown}{CE}.
\)
Сократим:
\(
\angle CAE = \frac{1}{2} (\overset{\frown}{CE} — \overset{\frown}{BD}),
\)
что и требовалось доказать.

Дано: окружность \((O; r)\), \(AC\), \(AE\) — секущие.

Доказать:
\(
\angle CAE = \frac{1}{2} (\overset{\frown}{CE} — \overset{\frown}{BD}).
\)

Рассмотрим треугольник \(\triangle ACD\). По теореме о сумме углов треугольника:
\(
\angle A = 180^\circ — (\angle C + \angle D).
\)

Угол \(\angle D\) является смежным с \(\angle CDE\). Следовательно:
\(
\angle D = 180^\circ — \angle CDE.
\)

Угол \(\angle CDE\) — вписанный угол, опирающийся на дугу \(\overset{\frown}{CE}\). По свойству вписанного угла:
\(
\angle CDE = \frac{1}{2} \overset{\frown}{CE}.
\)

Подставим значение \(\angle CDE\) в выражение для \(\angle D\):
\(
\angle D = 180^\circ — \frac{1}{2} \overset{\frown}{CE}.
\)

Угол \(\angle C\) также является вписанным углом, опирающимся на дугу \(\overset{\frown}{BD}\). По свойству вписанного угла:
\(
\angle C = \frac{1}{2} \overset{\frown}{BD}.
\)

Теперь выразим угол \(\angle CAE\). По свойству угла между секущими:
\(
\angle CAE = 180^\circ — (\angle C + \angle D).
\)

Подставим значения \(\angle C\) и \(\angle D\):
\(
\angle CAE = 180^\circ — \left(\frac{1}{2} \overset{\frown}{BD} + \left(180^\circ — \frac{1}{2} \overset{\frown}{CE}\right)\right).
\)

Раскроем скобки:
\(
\angle CAE = 180^\circ — \frac{1}{2} \overset{\frown}{BD} — 180^\circ + \frac{1}{2} \overset{\frown}{CE}.
\)

Сократим одинаковые величины:
\(
\angle CAE = \frac{1}{2} (\overset{\frown}{CE} — \overset{\frown}{BD}).
\)

Таким образом, доказательство завершено.