
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 717 Атанасян — Подробные Ответы
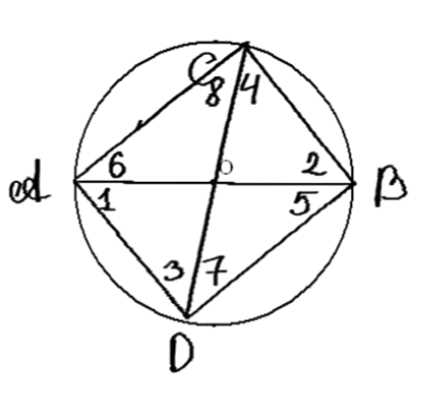
Отрезок \(AB\) является диаметром окружности, а хорды \(BC\) и \(AD\) параллельны. Докажите, что хорда \(CD\) является диаметром.
Дано:
Окружность \((O; r)\);
\(AB\) — диаметр;
\(BC \parallel AD\);
\(BC, AD\) — хорды.
Доказать: \(CD\) — диаметр.
Доказательство:
1) \(\angle DAB = \angle LABC\) (как накрестлежащие).
2) \(\angle DAB = \frac{\overset{\frown}{DB}}{2}\), \(\angle LABC = \frac{\overset{\frown}{AC}}{2}\) (как вписанные углы).
Так как \(\angle DAB = \angle LABC\), то \(\overset{\frown}{DB} = \overset{\frown}{AC}\).
3) \(\angle ZADC = \frac{\overset{\frown}{AC}}{2}\), \(\angle LDCB = \frac{\overset{\frown}{DB}}{2}\) (как вписанные углы).
4) \(\angle LADC = \angle LABC = \frac{\overset{\frown}{AC}}{2}\), \(\angle LDCB = \angle ZDAB = \frac{\overset{\frown}{DB}}{2}\).
Так как \(\overset{\frown}{DB} = \overset{\frown}{AC}\), то \(\angle LADC = \angle LABC = \angle LDCB = \angle ZDAB\).
Отсюда \(\triangle ADO\) и \(\triangle AOB\) — равнобедренные.
5) \(AO = OD\), \(OB = OC\).
Значит, \(DC = OD + OC = AO + OB = AB\).
Отсюда \(CD\) — диаметр, что и требовалось доказать.
Дано:
Окружность \((O; r)\);
\(AB\) — диаметр;
\(BC \parallel AD\);
\(BC\) и \(AD\) — хорды.
Доказать: \(CD\) — диаметр.
Доказательство:
1. Рассмотрим углы \(\angle DAB\) и \(\angle LABC\).
Эти углы являются накрестлежащими, так как \(BC \parallel AD\). Следовательно, \(\angle DAB = \angle LABC\).
2. Углы \(\angle DAB\) и \(\angle LABC\) являются вписанными углами, опирающимися на дуги \(\overset{\frown}{DB}\) и \(\overset{\frown}{AC}\) соответственно.
По свойству вписанных углов:
\(
\angle DAB = \frac{\overset{\frown}{DB}}{2}, \quad \angle LABC = \frac{\overset{\frown}{AC}}{2}.
\)
Так как \(\angle DAB = \angle LABC\), то:
\(
\frac{\overset{\frown}{DB}}{2} = \frac{\overset{\frown}{AC}}{2}.
\)
Умножим обе части равенства на \(2\):
\(
\overset{\frown}{DB} = \overset{\frown}{AC}.
\)
3. Рассмотрим углы \(\angle ZADC\) и \(\angle LDCB\).
Эти углы также являются вписанными и опираются на дуги \(\overset{\frown}{AC}\) и \(\overset{\frown}{DB}\) соответственно.
По свойству вписанных углов:
\(
\angle ZADC = \frac{\overset{\frown}{AC}}{2}, \quad \angle LDCB = \frac{\overset{\frown}{DB}}{2}.
\)
Так как \(\overset{\frown}{DB} = \overset{\frown}{AC}\), то:
\(
\frac{\overset{\frown}{AC}}{2} = \frac{\overset{\frown}{DB}}{2}.
\)
Отсюда:
\(
\angle ZADC = \angle LDCB.
\)
4. Теперь рассмотрим равенство углов:
\(
\angle LADC = \angle LABC = \frac{\overset{\frown}{AC}}{2}, \quad \angle LDCB = \angle ZDAB = \frac{\overset{\frown}{DB}}{2}.
\)
Так как \(\overset{\frown}{DB} = \overset{\frown}{AC}\), то:
\(
\angle LADC = \angle LABC, \quad \angle LDCB = \angle ZDAB.
\)
Следовательно, треугольники \(\triangle ADO\) и \(\triangle AOB\) являются равнобедренными.
5. Радиусы окружности равны:
\(
AO = OD, \quad OB = OC.
\)
Сложим эти равенства:
\(
DC = OD + OC = AO + OB.
\)
Так как \(AB\) — диаметр, то \(AO + OB = AB\).
Отсюда:
\(
DC = AB.
\)
Следовательно, \(CD\) — диаметр, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!