
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 715 Атанасян — Подробные Ответы
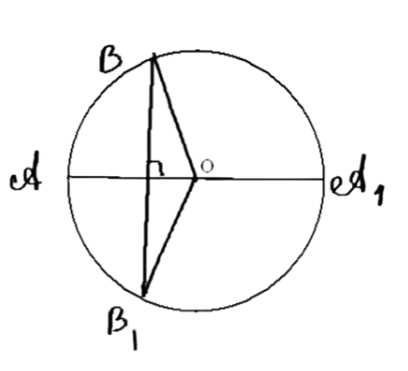
Диаметр \(AA_1\) окружности перпендикулярен к хорде \(BB_1\). Докажите, что градусные меры дуг \(AB\) и \(AB_1\), меньших полуокружности, равны.
Дано: \(BO = OB_1 = r\), \(AA_1 \perp BB_1\), \(\angle BDO = \angle ODB_1 = 90^\circ\).
Рассмотрим треугольники \(\triangle BDO\) и \(\triangle ODB_1\):
\(BO = OB_1\) (равные радиусы), \(DO\) — общий катет.
Следовательно, \(\triangle BDO = \triangle ODB_1\) по гипотенузе и катету, а значит, \(\angle BOD = \angle DOB_1\).
Центральные углы \(\angle BOD\) и \(\angle DOB_1\) соответствуют дугам \(\widehat{AB}\) и \(\widehat{AB_1}\).
Так как \(\angle BOD = \angle DOB_1\), то \(\widehat{AB} = \widehat{AB_1}\).
Доказано.
Дано:
Окружность \((O; r)\), где \(O\) — центр окружности, \(r\) — радиус.
\(AA_1\) — диаметр окружности, \(BB_1\) — хорда, причем \(AA_1 \perp BB_1\).
Требуется доказать, что дуги \(\widehat{AB}\) и \(\widehat{AB_1}\) равны, то есть \(\widehat{AB} = \widehat{AB_1}\).
Решение:
1) Рассмотрим треугольник \(\triangle BOB_1\). Радиусы \(BO\) и \(OB_1\) равны, так как оба являются радиусами данной окружности. Следовательно, треугольник \(\triangle BOB_1\) равнобедренный.
2) Диаметр \(AA_1\) перпендикулярен хорде \(BB_1\), значит углы при точке пересечения \(O\) равны \(90^\circ\). То есть, \(\angle BDO = \angle ODB_1 = 90^\circ\).
3) Рассмотрим треугольники \(\triangle BDO\) и \(\triangle ODB_1\). Они прямоугольные, а также:
— \(BO = OB_1\) (радиусы окружности);
— \(DO\) — общий катет.
Следовательно, треугольники \(\triangle BDO\) и \(\triangle ODB_1\) равны по гипотенузе и катету. Из равенства треугольников следует, что углы \(\angle BOD\) и \(\angle DOB_1\) равны, то есть \(\angle BOD = \angle DOB_1\).
4) Углы \(\angle BOD\) и \(\angle DOB_1\) являются центральными углами, которые опираются на дуги \(\widehat{AB}\) и \(\widehat{AB_1}\) соответственно.
Так как \(\angle BOD = \angle DOB_1\), то дуги \(\widehat{AB}\) и \(\widehat{AB_1}\) равны, то есть \(\widehat{AB} = \widehat{AB_1}\).
Ответ: доказано, что \(\widehat{AB} = \widehat{AB_1}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!