ГДЗ по Геометрии 8 класс Номер 714 Атанасян — Подробные Ответы

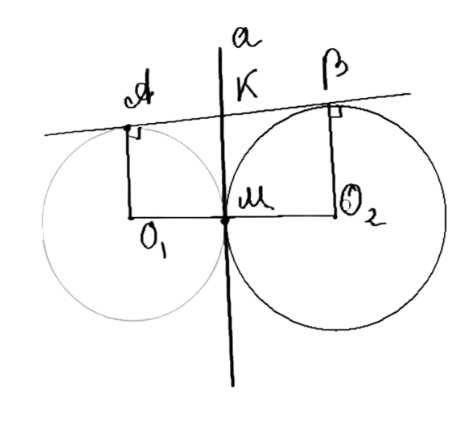
Две окружности имеют общую точку \(M\) и общую касательную в этой точке. Прямая \(AB\) касается одной окружности в точке \(A\), а другой — в точке \(B\). Докажите, что точка \(M\) лежит на окружности с диаметром \(AB\).

Дано: окружности \((O_1; r_1)\) и \((O_2; r_2)\) пересекаются в точке \(M\), касательная \(a\) проходит через \(M\), \(AB\) — общая касательная. Требуется доказать, что \(M \in (K; \frac{AB}{2})\).

Решение:
Пусть \(K = a \cap AB\). По свойству касательных из одной точки: \(AK = KM\) и \(KB = KM\), следовательно, \(AK = KM = KB\). Таким образом, \(AB = AK + KB = 2KM\), а радиус окружности с центром в \(K\) равен \(\frac{AB}{2}\). Точка \(M\) принадлежит этой окружности, что и требовалось доказать.

Дано: две окружности \((O_1; r_1)\) и \((O_2; r_2)\) пересекаются в точке \(M\). Проведена касательная \(a\), проходящая через точку \(M\), а также общая касательная \(AB\). Требуется доказать, что точка \(M\) принадлежит окружности с центром в точке \(K\) и радиусом \(\frac{AB}{2}\), где \(K\) — точка пересечения касательной \(a\) и прямой \(AB\).

Решение:

1. Проведем касательную \(a\) через точку \(M\) и обозначим точку пересечения касательной \(a\) и прямой \(AB\) как \(K\), то есть \(K = a \cap AB\).

2. Согласно свойству касательных, проведенных из одной точки, длины отрезков \(AK\) и \(KB\), образованных касательной \(AB\), равны между собой. Также длины отрезков \(AK\) и \(KM\), образованных касательной \(a\), равны между собой. Таким образом:
\(
AK = KM \quad \text{и} \quad KB = KM.
\)

3. Из равенства \(AK = KM = KB\) следует, что точки \(A\), \(M\), \(B\) лежат на окружности с центром в точке \(K\) и радиусом \(KM\).

4. Длина отрезка \(AB\) равна сумме длин отрезков \(AK\) и \(KB\):
\(
AB = AK + KB.
\)
Подставляя равенства \(AK = KM\) и \(KB = KM\), получаем:
\(
AB = KM + KM = 2KM.
\)

5. Радиус окружности с центром в точке \(K\) равен половине длины отрезка \(AB\):
\(
KM = \frac{AB}{2}.
\)

6. Таким образом, точка \(M\) принадлежит окружности с центром в точке \(K\) и радиусом \(\frac{AB}{2}\):
\(
M \in (K; \frac{AB}{2}).
\)

Ответ: точка \(M\) принадлежит окружности с центром в \(K\) и радиусом \(\frac{AB}{2}\), что и требовалось доказать.