
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 713 Атанасян — Подробные Ответы
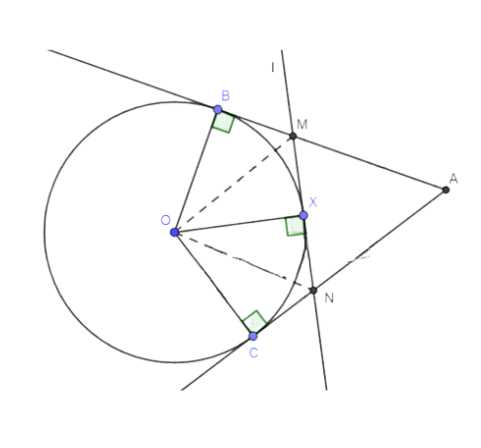
Прямые \(AB\) и \(AC\) — касательные к окружности с центром \(O\), \(B\) и \(C\) — точки касания. Через произвольную точку \(X\), взятую на дуге \(BC\), проведена касательная к этой окружности, пересекающая отрезки \(AB\) и \(AC\) в точках \(M\) и \(N\). Докажите, что периметр треугольника \(AMN\) и величина угла \(\angle MON\) не зависят от выбора точки \(X\) на дуге \(BC\).
Дано: окружность \((O; r)\), \(X \in BC\), \(X \in l\), \(AC\) и \(BC\) — касательные, \(AB \cap l = M\), \(AC \cap l = N\).
Доказать: \(P_{AMN}\), \(\angle MON\) не зависят от точки \(X\).
Решение:
1. Периметр треугольника \(P_{AMN}\) выражается как сумма сторон:
\(
P_{AMN} = AM + AN + MN.
\)
2. По свойству касательных:
\(
BM = MX, \quad XN = NC.
\)
3. Подставим в выражение для периметра:
\(
P_{AMN} = AM + AN + MX + XN = \)
\(=AM + AN + BM + NC = AB + AC.
\)
Таким образом, \(P_{AMN}\) не зависит от точки \(X\).
4. Угол \(\angle MON\) разбивается на сумму углов:
\(
\angle MON = \angle MOX + \angle XON.
\)
5. Рассмотрим треугольники \(\triangle BOM\) и \(\triangle MOX\):
\(
BM = MX, \quad MO \text{ — общая гипотенуза}.
\)
Следовательно, \(\triangle BOM = \triangle MOX\) (по гипотенузе и катету), отсюда:
\(
\angle MOX = \angle BOM.
\)
6. Рассмотрим треугольники \(\triangle NOX\) и \(\triangle NOC\):
\(
XN = NC, \quad NO \text{ — общая гипотенуза}.
\)
Следовательно, \(\triangle NOX = \triangle NOC\) (по гипотенузе и катету), отсюда:
\(
\angle XON = \angle NOC.
\)
7. Подставим в выражение для угла:
\(
\angle MON = \angle BOM + \angle NOC.
\)
Таким образом, \(\angle MON\) не зависит от точки \(X\), что и требовалось доказать.
Дано: окружность \((O; r)\), \(X \in BC\), \(X \in l\), \(AC\) и \(BC\) — касательные, \(AB \cap l = M\), \(AC \cap l = N\).
Доказать: \(P_{AMN}\), \(\angle MON\) не зависят от точки \(X\).
Решение:
1. Рассмотрим периметр треугольника \(P_{AMN}\). Периметр выражается как сумма длин сторон:
\(
P_{AMN} = AM + AN + MN.
\)
2. По свойству касательных к окружности из одной точки:
\(
BM = MX, \quad XN = NC.
\)
Это следует из того, что длины отрезков касательных, проведённых из одной точки к окружности, равны.
3. Выразим \(MN\) через \(MX\) и \(XN\):
\(
MN = MX + XN.
\)
Подставим это в формулу для периметра:
\(
P_{AMN} = AM + AN + MX + XN.
\)
4. Переставим слагаемые:
\(
P_{AMN} = AM + AN + BM + NC.
\)
Так как \(BM + AM = AB\) и \(NC + AN = AC\), то:
\(
P_{AMN} = AB + AC.
\)
Таким образом, периметр треугольника \(P_{AMN}\) равен сумме длин касательных \(AB\) и \(AC\), которые не зависят от точки \(X\).
5. Теперь докажем, что угол \(\angle MON\) не зависит от точки \(X\). Угол \(\angle MON\) можно представить как сумму двух углов:
\(
\angle MON = \angle MOX + \angle XON.
\)
6. Рассмотрим треугольники \(\triangle BOM\) и \(\triangle MOX\). В этих треугольниках:
\(
BM = MX, \quad MO \text{ — общая гипотенуза}.
\)
Следовательно, треугольники равны (\(\triangle BOM = \triangle MOX\)) по гипотенузе и катету. Из равенства треугольников следует равенство углов:
\(
\angle MOX = \angle BOM.
\)
7. Аналогично рассмотрим треугольники \(\triangle NOX\) и \(\triangle NOC\). В этих треугольниках:
\(
XN = NC, \quad NO \text{ — общая гипотенуза}.
\)
Следовательно, треугольники равны (\(\triangle NOX = \triangle NOC\)) по гипотенузе и катету. Из равенства треугольников следует равенство углов:
\(
\angle XON = \angle NOC.
\)
8. Подставим полученные равенства углов в выражение для \(\angle MON\):
\(
\angle MON = \angle BOM + \angle NOC.
\)
Так как углы \(\angle BOM\) и \(\angle NOC\) не зависят от точки \(X\), то и угол \(\angle MON\) не зависит от точки \(X\).
Ответ: периметр треугольника \(P_{AMN}\) и угол \(\angle MON\) не зависят от точки \(X\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!