Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 711 Атанасян — Подробные Ответы
Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. Для каждого из них постройте описанную окружность.
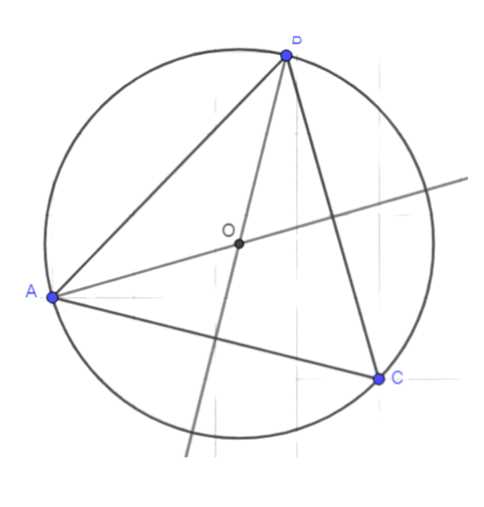
а) Для тупоугольного треугольника:
Строим медианы двух сторон, их пересечение дает центр окружности \(O\). Радиус окружности равен расстоянию от \(O\) до любой вершины треугольника.
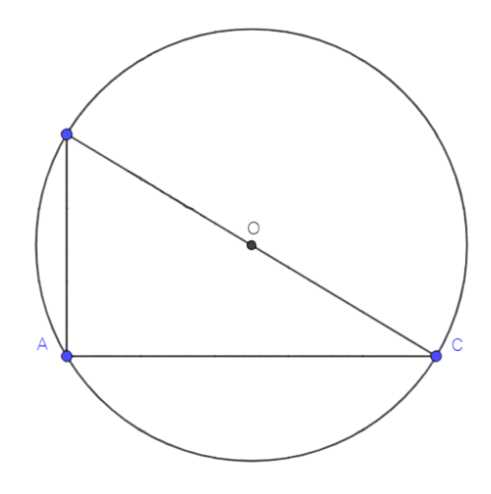
б) Для прямоугольного треугольника:
Центр окружности находится на середине гипотенузы \(O\). Радиус окружности равен половине длины гипотенузы.
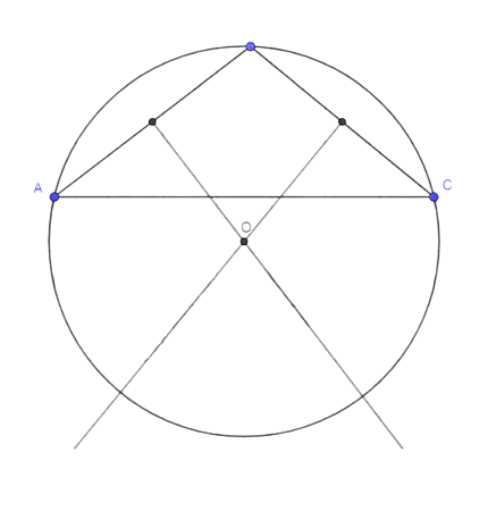
в) Для равностороннего треугольника:
Строим биссектриссы двух углов, их пересечение дает центр окружности \(O\). Радиус окружности равен расстоянию от \(O\) до любой вершины треугольника.
а) Для тупоугольного треугольника:
1. Находим медианы двух сторон треугольника. Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
2. Строим медианы для двух сторон треугольника.
3. Находим точку пересечения медиан. Эта точка является центром описанной окружности \(O\).
4. Измеряем расстояние от точки \(O\) до любой из вершин треугольника. Это расстояние является радиусом окружности \(OA\).
5. Строим окружность с центром в точке \(O\) и радиусом \(OA\).
б) Для прямоугольного треугольника:
1. В прямоугольном треугольнике центр описанной окружности всегда лежит на середине гипотенузы.
2. Находим середину гипотенузы, обозначаем эту точку как \(O\).
3. Измеряем длину гипотенузы и делим её на два. Полученное значение будет радиусом окружности \(OA\).
4. Строим окружность с центром \(O\) и радиусом \(OA\).
в) Для равностороннего треугольника:
1. В равностороннем треугольнике центр описанной окружности совпадает с точкой пересечения биссектрис, медиан и высот.
2. Строим биссектриссы двух углов треугольника. Биссектрисса — это отрезок, который делит угол пополам и соединяет вершину угла с противоположной стороной.
3. Находим точку пересечения биссектрис. Эта точка является центром окружности \(O\).
4. Измеряем расстояние от точки \(O\) до любой из вершин треугольника. Это расстояние является радиусом окружности \(OA\).
5. Строим окружность с центром в точке \(O\) и радиусом \(OA\).
Таким образом, описанная окружность строится для каждого типа треугольника с использованием указанных методов.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.