ГДЗ по Геометрии 8 класс Номер 701 Атанасян — Подробные Ответы

Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждый из них впишите окружность.

Дано треугольник.

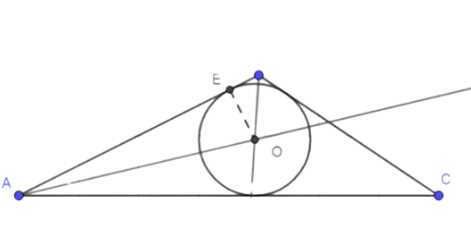
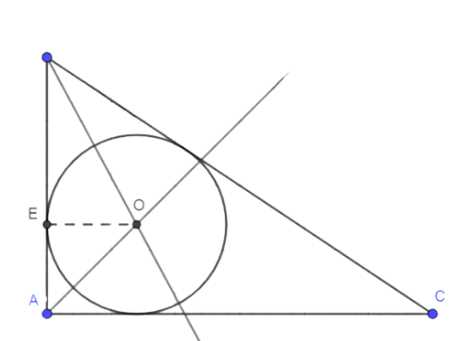
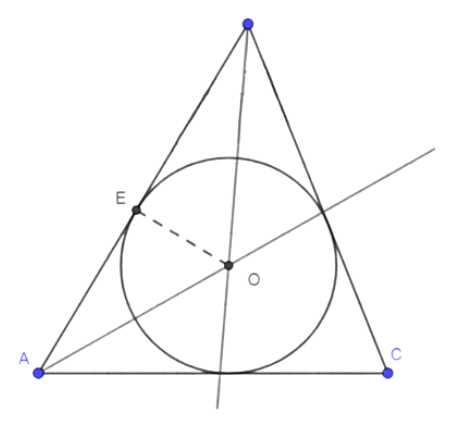
Для построения вписанной окружности:

1. Строим биссектриссы двух углов треугольника, их пересечение — центр окружности \(O\).

2. Из точки \(O\) восстанавливаем перпендикуляр к любой стороне треугольника, точка пересечения — точка \(E\).

3. Радиус окружности равен \(OE\), строим окружность с центром \(O\) и радиусом \(OE\).

Дано треугольник:
а) остроугольный;

б) прямоугольный;

в) тупоугольный.

Построить вписанную окружность.

Решение:

1. Вписанная окружность — это окружность, которая касается всех сторон треугольника. Центр вписанной окружности находится в точке пересечения биссектрис углов треугольника.

2. Построение:
а) Строим биссектриссы двух углов треугольника. Биссектрисса — это луч, который делит угол пополам. Пусть биссектриссы углов \( \angle A \) и \( \angle B \) пересекаются в точке \( O \). Точка \( O \) — центр вписанной окружности.

б) Из точки \( O \) восстанавливаем перпендикуляр к одной из сторон треугольника, например, к стороне \( BC \). Перпендикуляр пересекает сторону \( BC \) в точке \( E \).

в) Радиус вписанной окружности равен длине отрезка \( OE \).

г) Строим окружность с центром \( O \) и радиусом \( OE \).

3. Проверка:
Окружность касается всех сторон треугольника, так как радиус \( OE \) является расстоянием от центра окружности \( O \) до стороны \( BC \), а аналогичные расстояния до других сторон будут равны \( OE \).

Ответ: вписанная окружность построена.