
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 697 Атанасян — Подробные Ответы
Докажите, что площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
Доказать: Площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
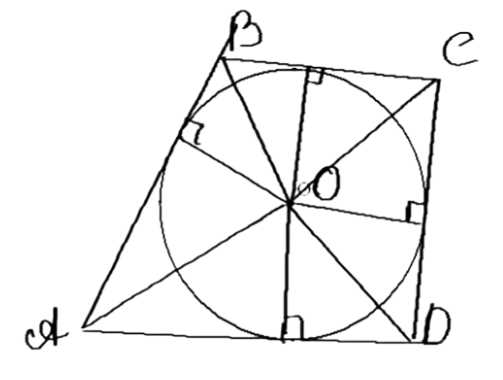
Центр вписанной окружности соединён с вершинами многоугольника, разделяя его на треугольники. В каждом треугольнике основание равно стороне многоугольника, а высота — радиус вписанной окружности \(r\).
Пусть \(a_1, a_2, \dots, a_n\) — стороны многоугольника, а \(S_1, S_2, \dots, S_n\) — площади треугольников. Тогда площадь многоугольника равна сумме площадей треугольников:
\(
S_{\text{многоуг}} = S_1 + S_2 + \dots + S_n.
\)
Площадь каждого треугольника вычисляется по формуле:
\(
S_i = \frac{1}{2} \cdot r \cdot a_i.
\)
Суммируя площади всех треугольников:
\(
S_{\text{многоуг}} = \frac{1}{2} \cdot r \cdot a_1 + \frac{1}{2} \cdot r \cdot a_2 + \dots + \frac{1}{2} \cdot r \cdot a_n=\)
\( = \frac{1}{2} \cdot r \cdot (a_1 + a_2 + \dots + a_n).
\)
Периметр многоугольника равен \(P = a_1 + a_2 + \dots + a_n\). Тогда:
\(
S = \frac{1}{2} \cdot r \cdot P.
\)
Что и требовалось доказать.
Доказать: площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
Рассмотрим произвольный многоугольник, вокруг которого описана окружность радиуса \( r \). Центр окружности соединён с вершинами многоугольника отрезками, которые делят его на \( n \) треугольников, где \( n \) — количество сторон многоугольника.
Пусть стороны многоугольника обозначены как \( a_1, a_2, \dots, a_n \), а площади треугольников — \( S_1, S_2, \dots, S_n \).
Площадь каждого треугольника можно вычислить по формуле:
\(
S_i = \frac{1}{2} \cdot r \cdot a_i,
\)
где \( a_i \) — сторона треугольника, совпадающая с одной из сторон многоугольника, а \( r \) — высота треугольника, равная радиусу вписанной окружности.
Сумма площадей всех треугольников даёт площадь многоугольника:
\(
S_{\text{многоуг}} = S_1 + S_2 + \dots + S_n.
\)
Подставим выражение для площади каждого треугольника:
\(
S_{\text{многоуг}} = \frac{1}{2} \cdot r \cdot a_1 + \frac{1}{2} \cdot r \cdot a_2 + \dots + \frac{1}{2} \cdot r \cdot a_n.
\)
Вынесем общий множитель \( \frac{1}{2} \cdot r \):
\(
S_{\text{многоуг}} = \frac{1}{2} \cdot r \cdot (a_1 + a_2 + \dots + a_n).
\)
Сумма всех сторон многоугольника равна его периметру:
\(
P = a_1 + a_2 + \dots + a_n.
\)
Таким образом, площадь многоугольника выражается как:
\(
S = \frac{1}{2} \cdot r \cdot P.
\)
Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!