
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 694 Атанасян — Подробные Ответы
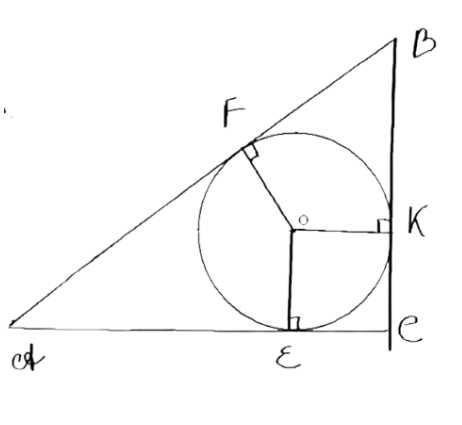
Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенуза треугольника равна \( c \), а сумма катетов равна \( m \).
Дано:
\(\triangle ABC\) — прямоугольный;
\(\angle C = 90^\circ;\)
\(AB = c;\)
\(AC + BC = m;\)
Решение:
По свойству касательных к окружности:
\(
AF = AD = x, \quad BD = BE = c — x, \quad FC = CE = r.
\)
Стороны треугольника выражаются как:
\(
AC = AF + FC = x + r, \quad BC = BE + EC = c — x + r.
\)
Сумма \(AC + BC = m\):
\(
x + r + c — x + r = m \quad \text{следовательно} \quad c + 2r = m.
\)
Отсюда:
\(
2r = m — c \quad \text{следовательно} \quad d = m — c.
\)
Ответ: \(d = m — c.\)
1) По свойству касательных к окружности:
\(
AF = AD, \, CF = CE, \, BD = BE.
\)
2) Радиус окружности:
\(
FC = CE = OE = FO = r.
\)
3) Пусть \(AD = AF = x\), тогда:
\(
BD = BE = c — x.
\)
4) Выразим стороны треугольника:
\(
AC = AF + FC = x + r, \quad BC = BE + EC = c — x + r.
\)
5) По условию задачи:
\(
AC + BC = m.
\)
Подставляем выражения для \(AC\) и \(BC\):
\(
x + r + c — x + r = m.
\)
Сокращаем:
\(
c + 2r = m.
\)
6) Выразим \(r\):
\(
2r = m — c.
\)
7) Радиус окружности совпадает с расстоянием \(d\) от точки \(D\) до окружности, следовательно:
\(
d = r.
\)
8) Подставляем значение \(r\):
\(
d = m — c.
\)
Ответ:
\(
d = m — c.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!