
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 691 Атанасян — Подробные Ответы
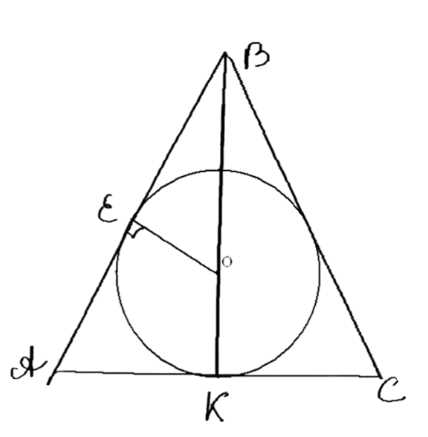
Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные \( 3 \, \text{см} \) и \( 4 \, \text{см} \), считая от основания. Найдите периметр треугольника.
Дано: треугольник \( \triangle ABC \) равнобедренный (\( AB = BC \)), \( BE = 4 \, \text{см} \), \( AE = 3 \, \text{см} \). Найти: \( P_{ABC} \).
Решение:
1. \( AB \) и \( AC \) — касательные к окружности, следовательно, \( AE = AK = 3 \, \text{см} \).
2. \( AB = BC = AE + BE = 3 + 4 = 7 \, \text{см} \).
3. \( BK \) — высота и медиана, поэтому \( AK = KC = 3 \, \text{см} \).
4. \( AC = AK + KC = 3 + 3 = 6 \, \text{см} \).
5. Периметр \( P_{ABC} = AB + AC + BC = 7 + 6 + 7 = 20 \, \text{см} \).
Ответ: \( P_{ABC} = 20 \, \text{см} \).
Дано: треугольник \( \triangle ABC \) равнобедренный (\( AB = BC \)), \( BE = 4 \, \text{см} \), \( AE = 3 \, \text{см} \). Найти: \( P_{ABC} \), где \( P_{ABC} \) — периметр треугольника.
Решение:
1. \( AB \) и \( AC \) — касательные к окружности в точках \( E \) и \( K \). Согласно свойству касательных, проведённых из одной точки, их длины равны. Следовательно:
\(
AE = AK = 3 \, \text{см}.
\)
2. Треугольник \( \triangle ABC \) равнобедренный (\( AB = BC \)). Длина стороны \( AB \) равна:
\(
AB = AE + BE = 3 + 4 = 7 \, \text{см}.
\)
Аналогично, \( BC = AB = 7 \, \text{см} \), так как треугольник равнобедренный.
3. Поскольку \( BK \) — высота и медиана (по свойству равнобедренного треугольника), то:
\(
AK = KC = 3 \, \text{см}.
\)
4. Найдём длину стороны \( AC \), которая состоит из двух равных частей (\( AK \) и \( KC \)):
\(
AC = AK + KC = 3 + 3 = 6 \, \text{см}.
\)
5. Периметр треугольника \( \triangle ABC \) вычисляется как сумма длин его сторон:
\(
P_{ABC} = AB + AC + BC = 7 + 6 + 7 = 20 \, \text{см}.
\)
Ответ:
\(
P_{ABC} = 20 \, \text{см}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!