
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 688 Атанасян — Подробные Ответы
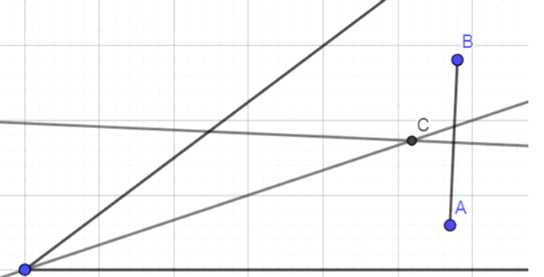
Даны угол и отрезок. Постройте точку, лежащую внутри данного угла, равноудалённую от его сторон и равноудалённую от концов данного отрезка.
Решение:
1. Построим серединный перпендикуляр к данному отрезку. Уравнение серединного перпендикуляра определяется через середину отрезка \((x_c, y_c)\) по формуле:
\(
y — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c).
\)
2. Построим биссектрису данного угла. Уравнение биссектрисы угла определяется геометрически, как линия, делящая угол пополам.
3. Найдем точку пересечения серединного перпендикуляра и биссектрисы. Для этого решим систему уравнений:
\(
y — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c),
\)
\(
y = kx + b.
\)
4. Точка пересечения является искомой точкой \(C\), равноудаленной от сторон угла и концов отрезка.
Дано: необходимо построить точку \(C\), которая лежит внутри угла, равноудалена от его сторон и равноудалена от концов данного отрезка.
Решение:
1. Построение серединного перпендикуляра к отрезку
Пусть даны точки \(A(x_1, y_1)\) и \(B(x_2, y_2)\), которые являются концами отрезка. Середина отрезка \(M(x_c, y_c)\) находится по формулам:
\(
x_c = \frac{x_1 + x_2}{2}, \quad y_c = \frac{y_1 + y_2}{2}.
\)
Уравнение серединного перпендикуляра строится через точку \(M(x_c, y_c)\) и имеет коэффициент наклона, обратный и противоположный наклону прямой, проходящей через точки \(A\) и \(B\). Коэффициент наклона прямой \(AB\):
\(
k_{AB} = \frac{y_2 — y_1}{x_2 — x_1}.
\)
Коэффициент наклона серединного перпендикуляра:
\(
k_{\text{перп}} = -\frac{1}{k_{AB}} = -\frac{x_2 — x_1}{y_2 — y_1}.
\)
Уравнение серединного перпендикуляра:
\(
y — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c).
\)
2. Построение биссектрисы угла
Пусть стороны угла заданы уравнениями прямых \(l_1: a_1x + b_1y + c_1 = 0\) и \(l_2: a_2x + b_2y + c_2 = 0\). Уравнение биссектрисы угла определяется как геометрическое место точек, равноудаленных от сторон:
\(
\frac{|a_1x + b_1y + c_1|}{\sqrt{a_1^2 + b_1^2}} = \frac{|a_2x + b_2y + c_2|}{\sqrt{a_2^2 + b_2^2}}.
\)
Раскрывая модули, получаем две биссектрисы (внутреннюю и внешнюю). Выбираем ту, которая проходит внутри угла.
3. Поиск точки пересечения серединного перпендикуляра и биссектрисы
Решаем систему уравнений, состоящую из уравнения серединного перпендикуляра:
\(
y — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c),
\)
и уравнения биссектрисы:
\(
\frac{|a_1x + b_1y + c_1|}{\sqrt{a_1^2 + b_1^2}} = \frac{|a_2x + b_2y + c_2|}{\sqrt{a_2^2 + b_2^2}}.
\)
Подставляем \(y\) из первого уравнения во второе и находим координаты точки пересечения \((x_C, y_C)\).
4. Искомая точка \(C\)
Точка \(C(x_C, y_C)\), найденная в предыдущем шаге, является искомой, так как она равноудалена от концов отрезка (по свойству серединного перпендикуляра) и равноудалена от сторон угла (по свойству биссектрисы).
Таким образом, точка \(C\) построена.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!