ГДЗ по Геометрии 8 класс Номер 687 Атанасян — Подробные Ответы

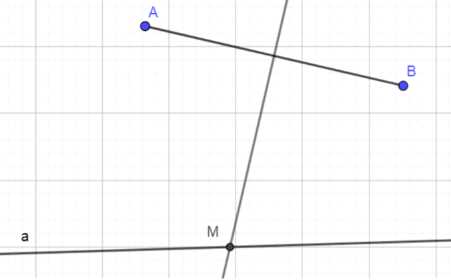
Даны прямая \( a \) и две точки \( A \) и \( B \), лежащие по одну сторону от этой прямой. На прямой \( a \) постройте точку \( M \), равноудалённую от точек \( A \) и \( B \).

Для построения точки \(M\), равноудаленной от \(A\) и \(B\):

1. Построим отрезок \(AB\).
2. Проведем серединный перпендикуляр к \(AB\), который проходит через середину отрезка и перпендикулярен ему.
3. Найдем точку пересечения серединного перпендикуляра и заданной прямой \(a\). Эта точка и будет искомой точкой \(M\).

Дано: необходимо построить точку \(M\), равноудаленную от точек \(A\) и \(B\), при этом точка \(M\) должна лежать на прямой \(a\).

Решение:

1. Построим отрезок \(AB\), соединяющий точки \(A(x_1, y_1)\) и \(B(x_2, y_2)\).

2. Найдем середину отрезка \(AB\). Координаты середины отрезка вычисляются по формуле:
\[
x_c = \frac{x_1 + x_2}{2}, \quad y_c = \frac{y_1 + y_2}{2}.
\]
Таким образом, середина \(C(x_c, y_c)\) имеет координаты:
\[
x_c = \frac{x_1 + x_2}{2}, \quad y_c = \frac{y_1 + y_2}{2}.
\]

3. Проведем серединный перпендикуляр к отрезку \(AB\). Уравнение серединного перпендикуляра будет иметь вид:
\[
y — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c),
\]
где \(-\frac{x_2 — x_1}{y_2 — y_1}\) — коэффициент наклона прямой, перпендикулярной отрезку \(AB\).

4. Запишем уравнение прямой \(a\), заданной в условии задачи. Пусть уравнение прямой \(a\) имеет вид:
\[
y = kx + b,
\]
где \(k\) — угловой коэффициент, а \(b\) — свободный член.

5. Найдем точку пересечения серединного перпендикуляра и прямой \(a\). Для этого решим систему уравнений:
\[
y — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c),
\]
\[
y = kx + b.
\]

6. Подставим выражение для \(y\) из второго уравнения в первое:
\[
kx + b — y_c = -\frac{x_2 — x_1}{y_2 — y_1}(x — x_c).
\]
Раскроем скобки и приведем подобные слагаемые:
\[
kx + b — y_c = -\frac{x_2 — x_1}{y_2 — y_1}x + \frac{x_2 — x_1}{y_2 — y_1}x_c.
\]
Сгруппируем все \(x\)-слагаемые:
\[
x\left(k + \frac{x_2 — x_1}{y_2 — y_1}\right) = y_c — b + \frac{x_2 — x_1}{y_2 — y_1}x_c.
\]
Выразим \(x\):
\[
x = \frac{y_c — b + \frac{x_2 — x_1}{y_2 — y_1}x_c}{k + \frac{x_2 — x_1}{y_2 — y_1}}.
\]

7. Найденное значение \(x\) подставим во второе уравнение для нахождения \(y\):
\[
y = kx + b.
\]

8. Таким образом, точка пересечения \(M(x, y)\) является искомой точкой, равноудаленной от \(A\) и \(B\) и лежащей на прямой \(a\).

Ответ: координаты точки \(M\) определяются решением системы уравнений серединного перпендикуляра и прямой \(a\).