ГДЗ по Геометрии 8 класс Номер 686 Атанасян — Подробные Ответы

Постройте серединный перпендикуляр к данному отрезку.  

Решение:  

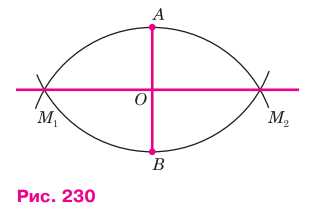
Пусть \( AB \) — данный отрезок. Построим две окружности с центрами в точках \( A \) и \( B \) радиуса \( AB \) (рис. 230). Эти окружности пересекаются в двух точках \( M_1 \) и \( M_2 \). Отрезки \( AM_1 \), \( AM_2 \), \( BM_1 \), \( BM_2 \) равны друг другу как радиусы этих окружностей.  

Проведём прямую \( M_1M_2 \). Она является искомым серединным перпендикуляром к отрезку \( AB \). В самом деле, точки \( M_1 \) и \( M_2 \) равноудалены от концов отрезка \( AB \), поэтому они лежат на серединном перпендикуляре к этому отрезку. Значит, прямая \( M_1M_2 \) и есть серединный перпендикуляр к отрезку \( AB \).

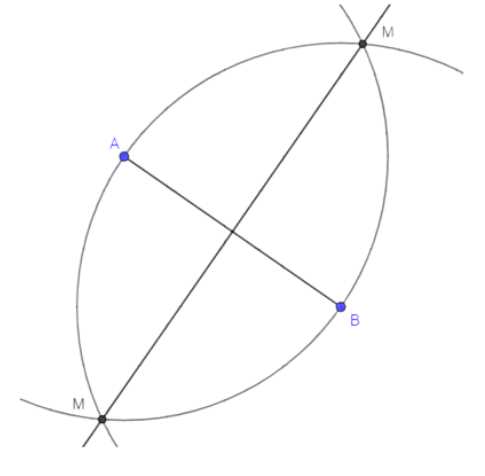
Для построения серединного перпендикуляра к \(AB\):

1. Построим окружности с центрами в точках \(A\) и \(B\), радиус которых равен длине отрезка \(AB\).
2. Найдем точки пересечения этих окружностей \(M\) и \(M_1\).
3. Проведем прямую \(MM_1\), которая будет серединным перпендикуляром к \(AB\).

Дано: необходимо построить серединный перпендикуляр к отрезку \(AB\).

Решение:

1. Построим окружность с центром в точке \(A\) и радиусом, равным длине отрезка \(AB\).
Уравнение окружности с центром \(A(x_1, y_1)\) и радиусом \(r = AB\) имеет вид:
\(
(x — x_1)^2 + (y — y_1)^2 = r^2
\)

2. Построим окружность с центром в точке \(B\) и радиусом, равным длине отрезка \(AB\).
Уравнение окружности с центром \(B(x_2, y_2)\) и радиусом \(r = AB\) имеет вид:
\(
(x — x_2)^2 + (y — y_2)^2 = r^2
\)

3. Найдем точки пересечения этих окружностей. Решение системы уравнений:
\(
(x — x_1)^2 + (y — y_1)^2 = r^2
\)
\(
(x — x_2)^2 + (y — y_2)^2 = r^2
\)
дает две точки пересечения \(M(x_3, y_3)\) и \(M_1(x_4, y_4)\).

4. Проведем прямую \(MM_1\), которая проходит через точки \(M\) и \(M_1\).
Уравнение прямой через две точки \(M(x_3, y_3)\) и \(M_1(x_4, y_4)\) имеет вид:
\(
y — y_3 = \frac{y_4 — y_3}{x_4 — x_3}(x — x_3)
\)

5. Прямая \(MM_1\) является серединным перпендикуляром к отрезку \(AB\), так как она проходит через точки пересечения окружностей, построенных с одинаковым радиусом \(AB\), и перпендикулярна отрезку \(AB\).

Ответ: построенная прямая \(MM_1\) — искомый серединный перпендикуляр.