ГДЗ по Геометрии 8 класс Номер 684 Атанасян — Подробные Ответы

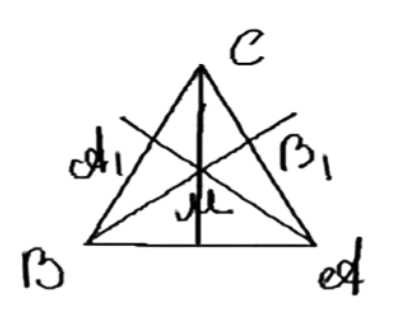
Биссектрисы углов при основании \( AB \) равнобедренного треугольника \( ABC \) пересекаются в точке \( M \). Докажите, что прямая \( CM \) перпендикулярна к прямой \( AB \).

Дано: \(\triangle ABC\), \(\angle ABC = \pi/6\), \(AC = CB\), \(AA_1\), \(BB_1\) — биссектрисы, \(AA_1 \cap BB_1 = M\).

Доказательство: \(CM\) является биссектрисой (по свойству пересечения биссектрис). Так как \(\triangle ABC\) равнобедренный (\(AC = CB\)), то биссектриса \(CM\) одновременно является высотой. Следовательно, \(CM \perp AB\), что и требовалось доказать.

Дано:
\(\triangle ABC\), \(\angle ABC = \pi/6\), \(AC = CB\), \(AA_1\), \(BB_1\) — биссектрисы, \(AA_1 \cap BB_1 = M\).

Необходимо доказать, что \(CM \perp AB\).

Рассмотрим решение:

1. По условию \(AA_1\) и \(BB_1\) являются биссектрисами треугольника, а точка \(M\) — их пересечение. Следовательно, \(CM\) также является биссектрисой (по свойству пересечения биссектрис треугольника).

2. Треугольник \(\triangle ABC\) равнобедренный, так как \(AC = CB\). В равнобедренном треугольнике биссектриса, проведённая из вершины угла при основании, является одновременно медианой и высотой.

3. Поскольку \(CM\) является биссектрисой угла \(\triangle ABC\), а треугольник равнобедренный, то \(CM\) также является высотой.

4. Высота треугольника проходит перпендикулярно основанию. Следовательно, \(CM \perp AB\).

Таким образом, доказано, что \(CM \perp AB\).