
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 682 Атанасян — Подробные Ответы
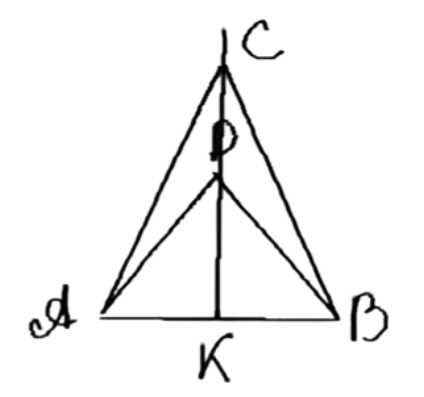
Равнобедренные треугольники \( ABC \) и \( ABD \) имеют общее основание \( AB \). Докажите, что прямая \( CD \) проходит через середину отрезка \( AB \).
Дано:
\(\triangle ABC\) и \(\triangle ABD\) равнобедренные, \(AB\) — основание.
Доказательство:
1) В \(\triangle ABC\) \(AC = CB\) (по свойству равнобедренного треугольника), следовательно, \(CK\) — серединный перпендикуляр к \(AB\).
2) В \(\triangle ABD\) \(AD = DB\), следовательно, \(CK\) также является серединным перпендикуляром к \(AB\).
3) Так как точки \(C\) и \(D\) принадлежат серединному перпендикуляру, то \(AK = KB\), а также \(CD \perp AB\).
Ответ: доказано.
Дано:
\(\triangle ABC\) и \(\triangle ABD\) равнобедренные, \(AB\) — основание.
Доказательство:
1) Рассмотрим \(\triangle ABC\). Так как он равнобедренный, то его боковые стороны равны:
\(
AC = CB
\)
По свойству равнобедренного треугольника, высота, проведенная из вершины \(C\) к основанию \(AB\), является одновременно медианой и серединным перпендикуляром. Следовательно, прямая \(CK\) — серединный перпендикуляр к \(AB\).
2) Рассмотрим \(\triangle ABD\). Так как он также равнобедренный, то его боковые стороны равны:
\(
AD = DB
\)
Аналогично, высота, проведенная из вершины \(D\) к основанию \(AB\), является медианой и серединным перпендикуляром. Следовательно, прямая \(CK\) одновременно является серединным перпендикуляром для обеих точек \(C\) и \(D\).
3) Так как точки \(C\) и \(D\) принадлежат серединному перпендикуляру \(CK\), то их проекции на прямую \(AB\) совпадают с точкой \(K\), которая делит отрезок \(AB\) на две равные части:
\(
AK = KB
\)
4) Далее, так как \(CK\) — серединный перпендикуляр, то он перпендикулярен основанию \(AB\). Следовательно, прямая \(CD\), проходящая через точки \(C\) и \(D\), также перпендикулярна основанию \(AB\):
\(
CD \perp AB
\)
Таким образом, доказано, что \(AK = KB\) и \(CD \perp AB\).
Ответ: доказано.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!