ГДЗ по Геометрии 8 класс Номер 675 Атанасян — Подробные Ответы

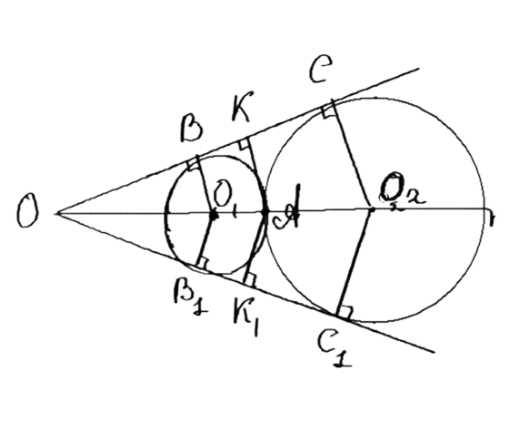
Стороны угла \( O \) касаются каждой из двух окружностей, имеющих общую касательную в точке \( A \). Докажите, что центры этих окружностей лежат на прямой \( OA \).

Дано: \( (O_1, R) \cap (O_2, r) = A \).

Доказательство:
\( BC \) и \( B_1C_1 \) — касательные к окружностям, значит \( O_1B \perp BC; O_2C \perp BC; O_1B_1 \perp B_1C_1; O_2C_1 \perp B_1C_1 \). Следовательно, точки \( O_1 \) и \( O_2 \) лежат на биссектрисе \( OO_2 \) по свойству биссектрисы.

Так как \( AK = AK_1 \) (по свойству биссектрис), то \( A \in OO_2 \), что и требовалось доказать.

Дано: \( (O_1, R) \cap (O_2, r) = A \).

Необходимо доказать: \( O_1 \in OA \) и \( O_2 \in OA \).

Рассмотрим окружности \( (O_1, R) \) и \( (O_2, r) \). Точки пересечения окружностей \( A \) и касательные \( BC \), \( B_1C_1 \) играют ключевую роль в доказательстве.

1. \( BC \) и \( B_1C_1 \) — касательные к окружностям, следовательно, радиусы \( O_1B \) и \( O_2C \) перпендикулярны \( BC \), то есть:
\( O_1B \perp BC \quad \text{и} \quad O_2C \perp BC. \)
Аналогично радиусы \( O_1B_1 \) и \( O_2C_1 \) перпендикулярны \( B_1C_1 \):
\( O_1B_1 \perp B_1C_1 \quad \text{и} \quad O_2C_1 \perp B_1C_1. \)

2. Из свойств биссектрисы следует, что точки \( O_1 \) и \( O_2 \) лежат на биссектрисе угла \( OO_2 \), так как радиусы, проведенные к касательным, равны.

3. Рассмотрим отрезки \( AK \) и \( AK_1 \). По свойству биссектрисы они равны, то есть:
\( AK = AK_1. \)

4. Так как точка \( A \) лежит на биссектрисе \( OO_2 \), то она принадлежит прямой, проходящей через центры окружностей \( O_1 \) и \( O_2 \).

Таким образом, доказано, что \( O_1 \in OA \) и \( O_2 \in OA \).