ГДЗ по Геометрии 8 класс Номер 674 Атанасян — Подробные Ответы

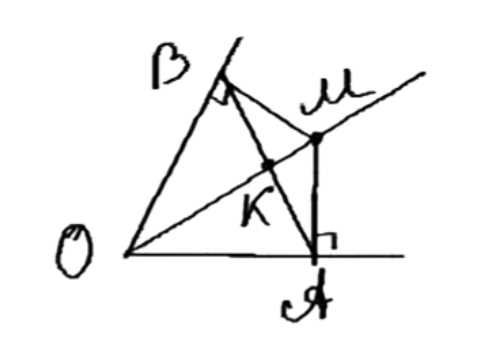
Из точки \( M \) биссектрисы неразвёрнутого угла \( O \) проведены перпендикуляры \( MA \) и \( MB \) к сторонам этого угла. Докажите, что \( AB \perp OM \).

Дано: \( \angle BOA; M \in OM, OM \) — биссектриса; \( MA \perp OA; MB \perp OB; AB \perp OM = K. \)
Доказать: \( AB \perp OM. \)

Рассмотрим треугольники \( \triangle OVM \) и \( \triangle OAM \). Они прямоугольные, \( \angle VOM = \angle MOA \), \( OM \) — общая гипотенуза. Следовательно, \( \triangle OVM = \triangle OAM \) по гипотенузе и острому углу. Отсюда \( OV = OA. \)

Так как \( OV = OA \), то \( \triangle OVA \) равнобедренный.

В равнобедренном треугольнике \( \triangle OVA \) биссектриса \( OK \) является высотой, то есть \( OK \perp AB. \) Следовательно, \( OM \perp AB. \) Доказано.

Дано: \( \angle BOA; M \in OM, OM \) — биссектриса; \( MA \perp OA; MB \perp OB; AB \perp OM = K. \)
Доказать: \( AB \perp OM. \)

Рассмотрим треугольники \( \triangle OVM \) и \( \triangle OAM \). Оба треугольника прямоугольные, так как \( MA \perp OA \) и \( MB \perp OB. \) У данных треугольников общий угол \( \angle VOM = \angle MOA, \) так как \( OM \) является биссектрисой угла \( \angle BOA. \) Также у треугольников общая гипотенуза \( OM. \)

По признаку равенства треугольников (гипотенуза и острый угол) получаем, что \( \triangle OVM = \triangle OAM. \) Следовательно, \( OV = OA. \)

Так как \( OV = OA, \) то треугольник \( \triangle OVA \) является равнобедренным.

В равнобедренном треугольнике \( \triangle OVA \) биссектриса \( OK \) одновременно является высотой, то есть \( OK \perp AB. \)

Так как \( OK \perp AB \), а \( OK \subset OM, \) то \( OM \perp AB. \)

Таким образом, доказано, что \( AB \perp OM. \)