
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 673 Атанасян — Подробные Ответы
К данной окружности постройте касательную, проходящую через данную точку вне окружности.
Решение:
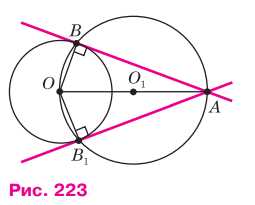
Пусть даны окружность с центром \( O \) и точка \( A \) вне этой окружности. Допустим, что задача решена и \( AB \) — искомая касательная (рис. 223). Так как прямая \( AB \) перпендикулярна к радиусу \( OB \), то решение задачи сводится к построению точки \( B \) окружности, для которой \( \angle ABO \) прямой. Эту точку можно построить следующим образом: проводим отрезок \( OA \) и строим его середину \( O_1 \). Затем проводим окружность с центром в точке \( O_1 \) радиуса \( O_1A \). Эта окружность пересекает данную окружность в двух точках: \( B \) и \( B_1 \). Прямые \( AB \) и \( AB_1 \) — искомые касательные, так как \( \angle ABO \) и \( \angle AB_1O \) — прямые. Действительно, углы \( \angle ABO \) и \( \angle AB_1O \), вписанные в окружность с центром \( O_1 \), опираются на полуокружности, поэтому они прямые. Очевидно, задача имеет два решения.
Дано: точка \(A\) вне окружности с центром \(O\). Требуется построить касательные к окружности, проходящие через точку \(A\).
Решение:
1. Построим отрезок \(OA\) и найдем его середину \(O_1\).
2. С центром в точке \(O_1\) и радиусом \(O_1A\) построим окружность.
3. Найдем точки пересечения новой окружности с исходной окружностью: точки \(B\) и \(B_1\).
4. Проведем прямые \(AB\) и \(AB_1\). Эти прямые являются искомыми касательными.
Решение завершено.
Дано: точка \(A\), находящаяся вне окружности с центром \(O\). Требуется построить касательные к окружности, проходящие через точку \(A\).
Решение:
1. Соединяем точку \(A\) с центром окружности \(O\). Получаем отрезок \(OA\).
2. Находим середину отрезка \(OA\). Для этого измеряем длину отрезка \(OA\) и делим её пополам. Обозначим середину отрезка как точку \(O_1\).
3. С центром в точке \(O_1\) и радиусом, равным половине длины отрезка \(OA\), строим окружность. Эта окружность называется вспомогательной.
4. Находим точки пересечения вспомогательной окружности с данной окружностью. Обозначим точки пересечения как \(B\) и \(B_1\).
5. Проводим прямую \(AB\), соединяющую точку \(A\) с точкой \(B\). Аналогично проводим прямую \(AB_1\), соединяющую точку \(A\) с точкой \(B_1\).
6. Доказываем, что прямые \(AB\) и \(AB_1\) являются касательными. Для этого нужно показать, что угол между радиусом окружности, проведенным в точку касания (например, \(OB\)), и касательной \(AB\) равен \(90^\circ\). Это следует из построения, так как точки \(B\) и \(B_1\) лежат на окружности, а расстояние \(O_1A\) равно радиусу вспомогательной окружности.
Таким образом, прямые \(AB\) и \(AB_1\) являются искомыми касательными.
Решение завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!