ГДЗ по Геометрии 8 класс Номер 672 Атанасян — Подробные Ответы

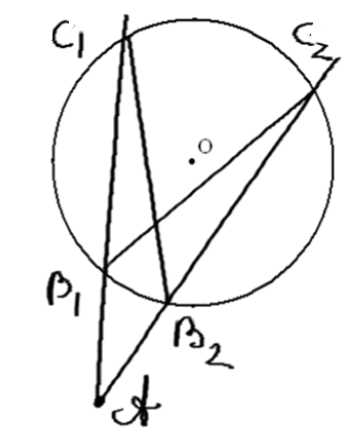
Через точку \( A \), лежащую вне окружности, проведены две секущие, одна из которых пересекает окружность в точках \( B_1 \) и \( C_1 \), а другая — в точках \( B_2 \) и \( C_2 \). Докажите, что \( AB_1 \cdot AC_1 = AB_2 \cdot AC_2 \).

Дано: окружность \((O; r)\), \(AC_1\) и \(AC_2\) — секущая, точки \(B_1, B_2, C_1, C_2\) принадлежат окружности.

Рассмотрим треугольники \(\triangle AC_1B_2\) и \(\triangle AC_2B_1\). У них общий угол \(\angle A\), а также углы \(\angle AC_2B_1\) и \(\angle AC_1B_2\) равны, так как оба составляют половину дуги \(\angle B_1B_2\).

По признаку подобия треугольников (\(\sim\) по двум углам):
\(
\frac{AC_1}{AC_2} = \frac{AB_2}{AB_1}.
\)

Умножая пропорцию на \(AC_2 \cdot AB_1\), получаем:
\(
AB_1 \cdot AC_1 = AB_2 \cdot AC_2.
\)

Доказано.

Дано:
Окружность \((O; r)\), \(AC_1\) и \(AC_2\) — секущая, точки \(B_1, B_2, C_1, C_2\) принадлежат окружности. Требуется доказать равенство:
\(
AB_1 \cdot AC_1 = AB_2 \cdot AC_2.
\)

Рассмотрим треугольники \(\triangle AC_1B_2\) и \(\triangle AC_2B_1\).

1. Общий угол:
У треугольников \(\triangle AC_1B_2\) и \(\triangle AC_2B_1\) угол \(\angle A\) является общим.

2. Равенство углов:
Углы \(\angle AC_1B_2\) и \(\angle AC_2B_1\) равны, так как оба составляют половину дуги \(\angle B_1B_2\):
\(
\angle AC_1B_2 = \angle AC_2B_1 = \frac{1}{2} \angle B_1B_2.
\)

3. Признак подобия:
Таким образом, треугольники \(\triangle AC_1B_2\) и \(\triangle AC_2B_1\) подобны по двум углам (\(\sim\)).

4. Пропорция сторон:
Из подобия следует пропорциональность соответствующих сторон:
\(
\frac{AC_1}{AC_2} = \frac{AB_2}{AB_1}.
\)

5. Умножение пропорции:
Умножим обе части пропорции на \(AC_2 \cdot AB_1\):
\(
AC_1 \cdot AB_1 = AC_2 \cdot AB_2.
\)

6. Вывод:
Таким образом, равенство доказано:
\(
AB_1 \cdot AC_1 = AB_2 \cdot AC_2.
\)

Доказательство завершено.