ГДЗ по Геометрии 8 класс Номер 668 Атанасян — Подробные Ответы

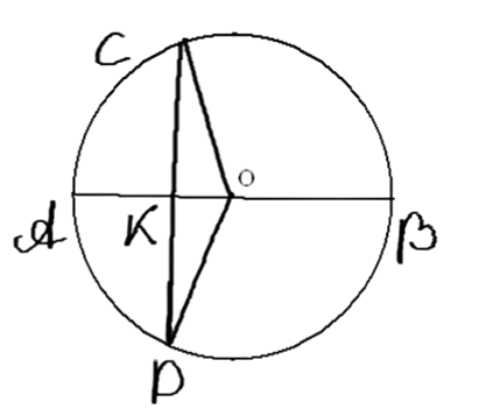
Докажите, что перпендикуляр, проведённый из какой-нибудь точки окружности к диаметру, есть среднее пропорциональное для отрезков, на которые основание перпендикуляра делит диаметр.

Дано: окружность \((O; r)\), \(AB\) — диаметр, \(AB \perp CD\), \(AB \cap CD = E\).

По свойству хорд:
\(
AE \cdot EB = CE \cdot ED
\)
Так как \(CO = OD = r\), то \(\triangle COD\) — равнобедренный, а \(OE\) — медиана, следовательно, \(CE = ED\). Подставляем в формулу:
\(
AE \cdot EB = CE^2 \quad \Rightarrow \quad CE = \sqrt{AE \cdot EB}.
\)

Доказано.

Дано: окружность \((O; r)\), \(AB\) — диаметр, \(AB \perp CD\), \(AB \cap CD = E\). Требуется доказать, что \(CE = \sqrt{AE \cdot EB}\).

Рассмотрим доказательство:

1. Так как \(CO = OD = r\), то \(\triangle COD\) является равнобедренным (по определению равнобедренного треугольника, у которого две стороны равны).

2. \(AB \perp CD\), следовательно, \(OE\) является высотой в \(\triangle COD\). Поскольку высота, проведённая к основанию равнобедренного треугольника, одновременно является медианой, то \(CE = ED\).

3. По свойству хорд, пересекающихся в окружности:
\(
AE \cdot EB = CE \cdot ED.
\)

4. Из пункта 2 следует, что \(CE = ED\). Подставим это равенство в формулу свойства хорд:
\(
AE \cdot EB = CE \cdot CE = CE^2.
\)

5. Возьмём квадратный корень из обеих частей равенства:
\(
CE = \sqrt{AE \cdot EB}.
\)

Таким образом, требуемое равенство доказано.