
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 664 Атанасян — Подробные Ответы
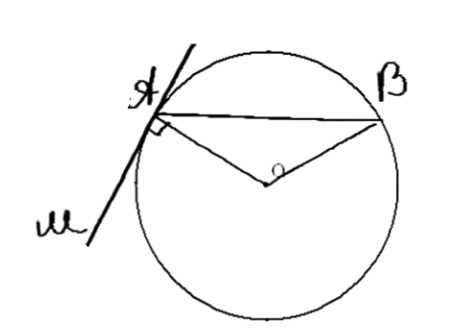
Прямая \( AM \) — касательная к окружности, \( AB \) — хорда этой окружности. Докажите, что угол \( \angle MAB \) измеряется половиной дуги \( AB \), расположенной внутри угла \( \angle MAB \).
Дано: \(AO = OB = r\), \(\triangle AOB\) — равнобедренный, отсюда \(\angle BAO = \angle ABO\).
Центральный угол \(\angle AOB = 180^\circ — 2\angle BAO\), и по теореме о центральном угле \(\angle AOB = \overset{\frown}{AB}\). Касательная \(AM \perp OA\), поэтому \(\angle MAB = 90^\circ — \angle BAO\). Подставляем: \(\angle AOB = 2(90^\circ — \angle BAO) = 2\angle MAB\). Следовательно, \(\overset{\frown}{AB} = 2\angle MAB\), значит \(\angle MAB = \frac{1}{2}\overset{\frown}{AB}\).
Дано: окружность с центром \(O\) и радиусом \(r\), хорда \(AB\), касательная \(AM\). Требуется доказать, что \(\angle MAB = \frac{1}{2} \overset{\frown}{AB}\).
Рассмотрим решение:
1. Радиусы \(AO\) и \(OB\) равны, так как они соединяют центр окружности с точками на окружности (\(AO = OB = r\)). Следовательно, треугольник \(\triangle AOB\) является равнобедренным. По свойству равнобедренного треугольника углы при основании равны:
\(
\angle BAO = \angle ABO.
\)
2. Центральный угол \(\angle AOB\) выражается через углы \(\angle BAO\) и \(\angle ABO\):
\(
\angle AOB = 180^\circ — \angle BAO — \angle ABO.
\)
Так как \(\angle BAO = \angle ABO\), то:
\(
\angle AOB = 180^\circ — 2\angle BAO.
\)
3. По теореме о центральном угле, центральный угол \(\angle AOB\) равен градусной мере дуги \(\overset{\frown}{AB}\):
\(
\angle AOB = \overset{\frown}{AB}.
\)
4. Касательная \(AM\) перпендикулярна радиусу \(OA\), проведённому в точку касания \(A\). Следовательно, угол между касательной \(AM\) и хордой \(AB\) выражается как:
\(
\angle MAB = 90^\circ — \angle BAO.
\)
5. Подставим выражение для \(\angle BAO\) из шага 2 в формулу для центрального угла:
\(
\angle AOB = 2(90^\circ — \angle BAO).
\)
Заметим, что \(90^\circ — \angle BAO = \angle MAB\), тогда:
\(
\angle AOB = 2\angle MAB.
\)
6. Так как \(\angle AOB = \overset{\frown}{AB}\), то:
\(
\overset{\frown}{AB} = 2\angle MAB.
\)
7. Отсюда следует, что:
\(
\angle MAB = \frac{1}{2} \overset{\frown}{AB}.
\)
Таким образом, утверждение доказано.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!