
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 658 Атанасян — Подробные Ответы
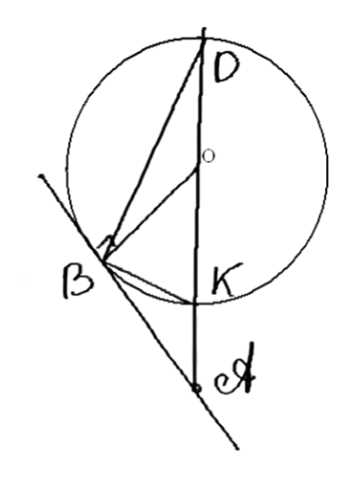
Через точку \( A \) к данной окружности проведены касательная \( AB \) (\( B \) — точка касания) и секущая \( AD \), проходящая через центр \( O \) (\( D \) — точка на окружности, \( O \) лежит между \( A \) и \( D \)). Найдите \( \angle BAD \) и \( \angle ADB \), если \( \angle CBD = 110^\circ 20′ \).
Дано:
Окр(\(O, R\)); \(AB\) — касательная; \(AD\) — секущая; \(\overset{\frown}{BD} = 110^\circ 20’\).
Найти: \(\angle BAD\), \(\angle ADB\).
Решение:
Вписанный угол \(\angle BKD\) равен половине дуги \(\overset{\frown}{BD}\):
\(
\angle BKD = \frac{1}{2} \cdot 110^\circ 20′ = 55^\circ 10′.
\)
Дуга \(\overset{\frown}{KD} = 180^\circ\), поэтому вписанный угол \(\angle DBK\):
\(
\angle DBK = \frac{1}{2} \cdot 180^\circ = 90^\circ.
\)
В треугольнике \(DBK\) угол \(\angle D\):
\(
\angle D = 180^\circ — \angle BKD — \angle DBK = 90^\circ — 55^\circ 10′ = 34^\circ 50′.
\)
Следовательно, \(\angle ADB = \angle D = 34^\circ 50’\).
Треугольник \(BOD\) равнобедренный (\(BO = OD = R\)), его углы \(\angle DBO = \angle BDO = 34^\circ 50’\).
Угол \(\angle DBA\):
\(
\angle DBA = \angle DBO + \angle OBA = 34^\circ 50′ + 90^\circ = 124^\circ 50′.
\)
Угол \(\angle BAD\):
\(
\angle BAD = 180^\circ — (\angle DBA + \angle ADB) = 180^\circ — (124^\circ 50′ + 34^\circ 50′) = 20^\circ 20′.
\)
Ответ:
\(\angle BAD = 20^\circ 20’\), \(\angle ADB = 34^\circ 50’\).
Дано:
Окружность с центром \(O\) и радиусом \(R\). Прямая \(AB\) — касательная к окружности, а \(AD\) — секущая. Дуга \(\overset{\frown}{BD}\) имеет градусную меру \(110^\circ 20’\).
Требуется найти углы \(\angle BAD\) и \(\angle ADB\).
Решение:
1. Вписанный угол \(\angle BKD\) опирается на дугу \(\overset{\frown}{BD}\) и равен половине её градусной меры:
\(
\angle BKD = \frac{1}{2} \cdot \overset{\frown}{BD}.
\)
Подставляем значение дуги:
\(
\angle BKD = \frac{1}{2} \cdot 110^\circ 20′ = 55^\circ 10′.
\)
2. Дуга \(\overset{\frown}{KD}\) является диаметральной, так как \(O\) — центр окружности и точка \(K\) лежит на прямой \(AD\). Следовательно, её градусная мера равна \(180^\circ\).
3. Вписанный угол \(\angle DBK\), опирающийся на дугу \(\overset{\frown}{KD}\), равен половине её градусной меры:
\(
\angle DBK = \frac{1}{2} \cdot \overset{\frown}{KD}.
\)
Подставляем значение дуги:
\(
\angle DBK = \frac{1}{2} \cdot 180^\circ = 90^\circ.
\)
4. Рассмотрим треугольник \(DBK\). Сумма углов треугольника равна \(180^\circ\). Угол \(\angle D\) можно найти, вычитая из \(180^\circ\) сумму углов \(\angle BKD\) и \(\angle DBK\):
\(
\angle D = 180^\circ — \angle BKD — \angle DBK.
\)
Подставляем значения:
\(
\angle D = 180^\circ — 55^\circ 10′ — 90^\circ = 34^\circ 50′.
\)
Следовательно, \(\angle ADB = \angle D = 34^\circ 50’\).
5. Рассмотрим треугольник \(BOD\). Так как \(BO = OD = R\), треугольник \(BOD\) является равнобедренным. Углы при основании равны:
\(
\angle DBO = \angle BDO = 34^\circ 50′.
\)
6. Угол \(\angle DBA\) состоит из двух частей:
\(
\angle DBA = \angle DBO + \angle OBA.
\)
Так как \(\angle OBA = 90^\circ\) (угол между радиусом и касательной), подставляем значения:
\(
\angle DBA = 34^\circ 50′ + 90^\circ = 124^\circ 50′.
\)
7. Угол \(\angle BAD\) можно найти, используя свойство треугольника \(ABD\), сумма углов которого равна \(180^\circ\):
\(
\angle BAD = 180^\circ — (\angle DBA + \angle ADB).
\)
Подставляем значения:
\(
\angle BAD = 180^\circ — (124^\circ 50′ + 34^\circ 50′) = 180^\circ — 159^\circ 40′ = 20^\circ 20′.
\)
Ответ:
\(\angle BAD = 20^\circ 20’\), \(\angle ADB = 34^\circ 50’\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!