Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 655 Атанасян — Подробные Ответы
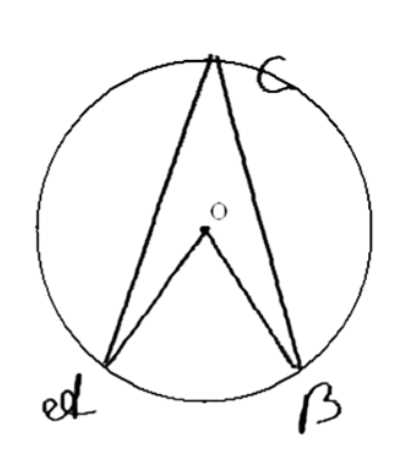
Центральный угол \( \angle AOB \) на \( 30^\circ \) больше вписанного угла, опирающегося на дугу \( AB \). Найдите каждый из этих углов.
Пусть \(\angle ACB = x\), тогда \(\angle AOB = x + 30^\circ\).
По теореме о вписанном угле:
\(
\angle ACB = \frac{1}{2} \angle AOB.
\)
Подставим:
\(
x = \frac{1}{2} (x + 30^\circ).
\)
Раскроем скобки:
\(
x = \frac{1}{2} x + 15^\circ.
\)
Переносим \(\frac{1}{2} x\) влево:
\(
x — \frac{1}{2} x = 15^\circ.
\)
Приводим подобные:
\(
\frac{1}{2} x = 15^\circ.
\)
Умножим на 2:
\(
x = 30^\circ.
\)
Значит, \(\angle ACB = 30^\circ\), а \(\angle AOB = x + 30^\circ = 60^\circ\).
Ответ: \(\angle ACB = 30^\circ\), \(\angle AOB = 60^\circ\).
Дано:
Окружность с центром \(O\) и радиусом \(R\).
\(\angle AOB = \angle ACB + 30^\circ\).
Найти:
\(\angle AOB\), \(\angle ACB\).
Решение:
1. Пусть \(\angle ACB = x\). Тогда из условия задачи:
\(
\angle AOB = x + 30^\circ.
\)
2. По теореме о вписанном угле:
\(
\angle AOB = 2 \angle AB.
\)
Поскольку \(\angle ACB\) является вписанным углом, опирающимся на ту же дугу \(AB\), то:
\(
\angle ACB = \frac{1}{2} \angle AOB.
\)
3. Подставим значение \(\angle AOB\) из условия задачи:
\(
\angle ACB = \frac{1}{2} (x + 30^\circ).
\)
4. Приравняем углы, так как \(\angle ACB = x\):
\(
x = \frac{1}{2} (x + 30^\circ).
\)
5. Раскроем скобки:
\(
x = \frac{1}{2} x + 15^\circ.
\)
6. Перенесем \(\frac{1}{2} x\) влево:
\(
x — \frac{1}{2} x = 15^\circ.
\)
7. Приведем подобные:
\(
\frac{1}{2} x = 15^\circ.
\)
8. Умножим обе части на 2:
\(
x = 30^\circ.
\)
9. Найдем \(\angle AOB\):
\(
\angle AOB = x + 30^\circ = 30^\circ + 30^\circ = 60^\circ.
\)
Ответ:
\(\angle ACB = 30^\circ\), \(\angle AOB = 60^\circ\).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.