
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 654 Атанасян — Подробные Ответы
По данным рисунка 222 найдите \( x \).
а)
\(
x = \frac{360^\circ — 152^\circ — 80^\circ}{2} = \frac{128^\circ}{2} = 64^\circ;
\)
б)
\(
x = 360^\circ — 125^\circ — 30^\circ \cdot 2 = 360^\circ — 185^\circ = 175^\circ;
\)
в)
\(
x = \frac{360^\circ — 112^\circ — 180^\circ}{2} = \frac{68^\circ}{2} = 34^\circ;
\)
г)
\(
x = 360^\circ — 215^\circ — 20^\circ \cdot 2 = 360^\circ — 255^\circ = 105^\circ;
\)
Ответ:
а) \(64^\circ\);
б) \(175^\circ\);
в) \(34^\circ\);
г) \(105^\circ\).
а)
Для вычисления значения угла \(x\), используем формулу для вписанного угла:
\(
x = \frac{360^\circ — \alpha — \beta}{2},
\)
где \(\alpha\) и \(\beta\) — известные углы. Подставляем значения:
\(
x = \frac{360^\circ — 152^\circ — 80^\circ}{2}.
\)
Выполним вычитание:
\(
360^\circ — 152^\circ = 208^\circ, \quad 208^\circ — 80^\circ = 128^\circ.
\)
Теперь делим результат на 2:
\(
x = \frac{128^\circ}{2} = 64^\circ.
\)
б)
Здесь угол \(x\) вычисляется по формуле:
\(
x = 360^\circ — \alpha — \beta \cdot 2,
\)
где \(\alpha = 125^\circ\), \(\beta = 30^\circ\). Подставляем значения:
\(
x = 360^\circ — 125^\circ — 30^\circ \cdot 2.
\)
Сначала умножим \(30^\circ\) на 2:
\(
30^\circ \cdot 2 = 60^\circ.
\)
Теперь выполним вычитание:
\(
360^\circ — 125^\circ = 235^\circ, \quad 235^\circ — 60^\circ = 175^\circ.
\)
Таким образом:
\(
x = 175^\circ.
\)
в)
Для вычисления угла \(x\) используем формулу для вписанного угла:
\(
x = \frac{360^\circ — \alpha — \beta}{2},
\)
где \(\alpha = 112^\circ\), \(\beta = 180^\circ\). Подставляем значения:
\(
x = \frac{360^\circ — 112^\circ — 180^\circ}{2}.
\)
Выполним вычитание:
\(
360^\circ — 112^\circ = 248^\circ, \quad 248^\circ — 180^\circ = 68^\circ.
\)
Теперь делим результат на 2:
\(
x = \frac{68^\circ}{2} = 34^\circ.
\)
г)
Для вычисления угла \(x\) используем формулу:
\(
x = 360^\circ — \alpha — \beta \cdot 2,
\)
где \(\alpha = 215^\circ\), \(\beta = 20^\circ\). Подставляем значения:
\(
x = 360^\circ — 215^\circ — 20^\circ \cdot 2.
\)
Сначала умножим \(20^\circ\) на 2:
\(
20^\circ \cdot 2 = 40^\circ.
\)
Теперь выполним вычитание:
\(
360^\circ — 215^\circ = 145^\circ, \quad 145^\circ — 40^\circ = 105^\circ.
\)
Таким образом:
\(
x = 105^\circ.
\)
Ответ:
а) \(64^\circ\);
б) \(175^\circ\);
в) \(34^\circ\);
г) \(105^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


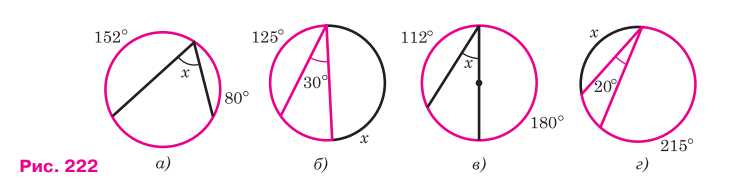

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!