
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 653 Атанасян — Подробные Ответы
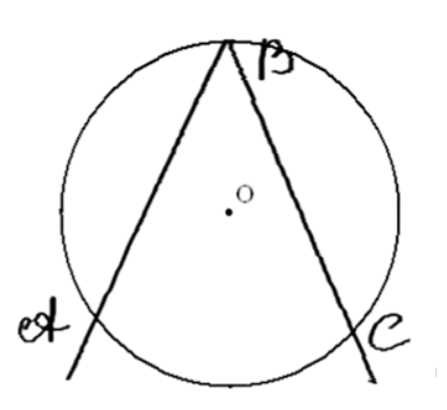
Найдите вписанный угол \( \angle ABC \), если дуга \( AC \), на которую он опирается, равна:
а) \( 48^\circ \);
б) \( 57^\circ \);
в) \( 90^\circ \);
г) \( 124^\circ \);
д) \( 180^\circ \).
Дано: \(\angle ABC\) — вписанный.
По теореме о вписанном угле:
\(
\angle ABC = \frac{1}{2} \angle AC.
\)
а) \(\angle AC = 48^\circ\), тогда:
\(
\angle ABC = \frac{48^\circ}{2} = 24^\circ.
\)
б) \(\angle AC = 57^\circ\), тогда:
\(
\angle ABC = \frac{57^\circ}{2} = 28^\circ 30′.
\)
в) \(\angle AC = 90^\circ\), тогда:
\(
\angle ABC = \frac{90^\circ}{2} = 45^\circ.
\)
г) \(\angle AC = 124^\circ\), тогда:
\(
\angle ABC = \frac{124^\circ}{2} = 62^\circ.
\)
д) \(\angle AC = 180^\circ\), тогда:
\(
\angle ABC = \frac{180^\circ}{2} = 90^\circ.
\)
Ответ:
а) \(24^\circ\);
б) \(28^\circ 30’\);
в) \(45^\circ\);
г) \(62^\circ\);
д) \(90^\circ\).
Дано: \(\angle ABC\) — вписанный угол.
Необходимо найти значение \(\angle ABC\).
Решение:
1. Согласно теореме о вписанном угле:
\(
\angle ABC = \frac{1}{2} \angle AC,
\)
где \(\angle AC\) — центральный угол, опирающийся на ту же дугу, что и вписанный угол \(\angle ABC\).
2. Рассмотрим заданные значения \(\angle AC\):
а) Если \(\angle AC = 48^\circ\), то:
\(
\angle ABC = \frac{48^\circ}{2} = 24^\circ.
\)
б) Если \(\angle AC = 57^\circ\), то:
\(
\angle ABC = \frac{57^\circ}{2} = 28^\circ 30′.
\)
Здесь дробь \(\frac{57}{2}\) представлена в виде смешанного числа \(28^\circ 30’\), так как \(57 \div 2 = 28\) целых и остаток \(1\), который составляет половину градуса (\(30’\)).
в) Если \(\angle AC = 90^\circ\), то:
\(
\angle ABC = \frac{90^\circ}{2} = 45^\circ.
\)
г) Если \(\angle AC = 124^\circ\), то:
\(
\angle ABC = \frac{124^\circ}{2} = 62^\circ.
\)
д) Если \(\angle AC = 180^\circ\), то:
\(
\angle ABC = \frac{180^\circ}{2} = 90^\circ.
\)
Ответ:
а) \(24^\circ\);
б) \(28^\circ 30’\);
в) \(45^\circ\);
г) \(62^\circ\);
д) \(90^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!