
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 648 Атанасян — Подробные Ответы
Постройте касательную к окружности с центром \( O \):
а) параллельную данной прямой;
б) перпендикулярную к данной прямой.
Для построения касательных:
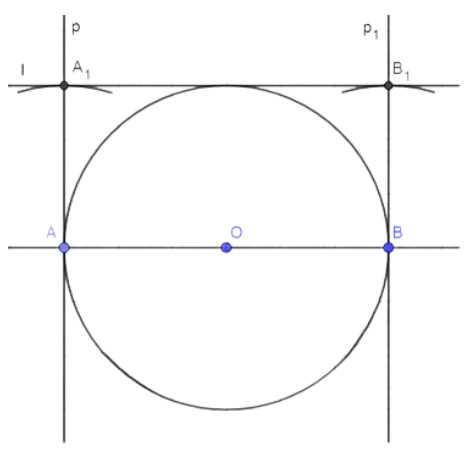
а) Чтобы построить касательную \(l \parallel AB\), через точки \(A\) и \(B\) проведем прямые \(p\) и \(p_1\), перпендикулярные к \(AB\). На этих прямых отложим отрезки \(AA_1\) и \(BB_1\), равные радиусу окружности (\(AO\)). Соединим точки \(A_1\) и \(B_1\), получив прямую \(l\).
б) Чтобы построить касательную \(p \perp AB\), через каждую из точек \(A\) и \(B\) проведем прямые \(p\) и \(p_1\), перпендикулярные \(AB\). Эти прямые и будут искомыми касательными.
Рассмотрим задачу по построению касательных к окружности. Требуется построить:
а) касательную \( l \parallel AB \);
б) касательную \( p \perp AB \).
Решение:
1. Для начала определим основные параметры окружности. Пусть радиус окружности равен \( AO \), где \( O \) — центр окружности, а \( A \) и \( B \) — две точки на окружности.
2. Построение касательной \( l \parallel AB \):
а) Через точки \( A \) и \( B \) проведем прямые \( p \) и \( p_1 \), которые перпендикулярны отрезку \( AB \). Это делается с помощью построения прямых под углом \( 90^\circ \) к отрезку \( AB \) в точках \( A \) и \( B \).
б) На прямых \( p \) и \( p_1 \) отложим отрезки \( AA_1 \) и \( BB_1 \), равные радиусу окружности \( AO \). Таким образом, точки \( A_1 \) и \( B_1 \) будут находиться на расстоянии, равном радиусу окружности, от точек \( A \) и \( B \).
в) Соединим точки \( A_1 \) и \( B_1 \). Полученная прямая \( l \) будет касательной, параллельной отрезку \( AB \).
3. Построение касательной \( p \perp AB \):
а) Проведем через точки \( A \) и \( B \) прямые \( p \) и \( p_1 \), которые перпендикулярны отрезку \( AB \). Это те же прямые, которые были построены на предыдущем этапе.
б) Эти прямые \( p \) и \( p_1 \) автоматически будут касательными к окружности, так как они проходят через точки \( A \) и \( B \), лежащие на окружности, и перпендикулярны радиусам \( AO \) и \( BO \), проведенным к этим точкам.
Таким образом, мы получили:
1) Касательная \( l \parallel AB \) — это прямая, соединяющая точки \( A_1 \) и \( B_1 \), находящиеся на расстоянии радиуса окружности от точек \( A \) и \( B \).
2) Касательные \( p \) и \( p_1 \) — это прямые, перпендикулярные отрезку \( AB \), проведенные через точки \( A \) и \( B \).
Построение завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!