ГДЗ по Геометрии 8 класс Номер 644 Атанасян — Подробные Ответы

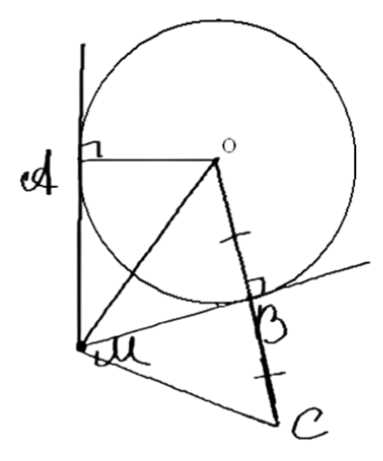
Прямые \( MA \) и \( MB \) касаются окружности с центром \( O \) в точках \( A \) и \( B \). Точка \( C \) симметрична точке \( O \) относительно точки \( B \). Докажите, что \( \angle AMC = 2 \angle BMC \).

Дано: окружность \(O, R\); \(BM\) и \(AM\) — касательные; \(OB = BC\).

Докажем, что \(\angle AMC = 3 \angle BMC\).

Рассмотрим \(\triangle OMB\) и \(\triangle CMB\), они прямоугольные, так как \(BM\) — общая сторона и \(OB = BC\) (по условию). Следовательно, \(\triangle OMB = \triangle CMB\) (по двум катетам), отсюда \(\angle OMB = \angle CMB\).

По свойству катетов \(\angle BMO = \angle AMO\).

Запишем \(\angle AMC\) через сумму углов:
\(
\angle AMC = \angle AMO + \angle BMC + \angle OMB.
\)

Так как \(\angle OMB = \angle CMB = \angle AMO\), то
\(
\angle AMC = 3 \angle BMC.
\)

Что и требовалось доказать.

Дано: окружность с центром \(O\) и радиусом \(R\); \(BM\) и \(AM\) — касательные к окружности; \(OB = BC\).

Требуется доказать, что \(\angle AMC = 3 \angle BMC\).

Рассмотрим решение:

1. Треугольники \(\triangle OMB\) и \(\triangle CMB\) являются прямоугольными, так как \(BM\) — общая сторона, а \(OB = BC\) (по условию).
Следовательно, треугольники \(\triangle OMB\) и \(\triangle CMB\) равны по двум катетам. Из равенства треугольников следует, что \(\angle OMB = \angle CMB\).

2. Углы \(\angle BMO\) и \(\angle AMO\) равны, так как они опираются на радиусы окружности, проведённые к точкам касания \(B\) и \(A\).

3. Угол \(\angle AMC\) можно выразить как сумму углов:
\(
\angle AMC = \angle AMO + \angle BMC + \angle OMB.
\)

4. Из равенства треугольников \(\triangle OMB\) и \(\triangle CMB\) следует, что \(\angle OMB = \angle CMB = \angle AMO\).
Поэтому угол \(\angle AMC\) можно записать как:
\(
\angle AMC = \angle AMO + \angle AMO + \angle AMO.
\)

5. Таким образом, \(\angle AMC = 3 \angle AMO\). А так как \(\angle AMO = \angle BMC\), то:
\(
\angle AMC = 3 \angle BMC.
\)

Что и требовалось доказать.