
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 637 Атанасян — Подробные Ответы
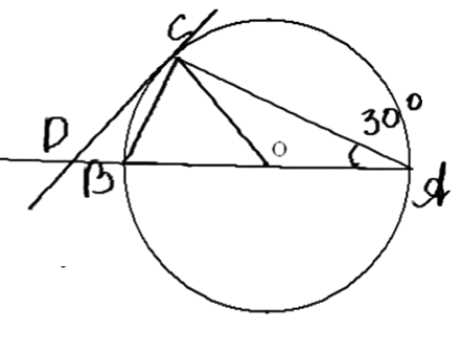
Угол между диаметром \( AB \) и хордой \( AC \) равен \( 30^\circ \). Через точку \( C \) проведена касательная, пересекающая прямую \( AB \) в точке \( D \). Докажите, что треугольник \( ACD \) равнобедренный.
Дано: \(p\) — касательная, \(AB\) — диаметр, \(AC = r\), \(p \cap AB = D\).
Доказать: \(\triangle ACD = \frac{\pi}{6}\).
Рассмотрим \(\triangle AOC\): \(OA = OC\) (радиусы), значит \(\triangle AOC\) равнобедренный, следовательно, \(\angle OCA = \angle OAC = 30^\circ\).
Угол \(\angle BOC\) — внешний, следовательно, \(\angle BOC = 30^\circ + 30^\circ = 60^\circ\).
В прямоугольном треугольнике \(\triangle OCD\): \(\angle CDO = 90^\circ — \angle BOC = 90^\circ — 60^\circ = 30^\circ\).
В треугольнике \(\triangle ACD\): \(\angle A = \angle D = 30^\circ\), значит \(\triangle ACD\) равнобедренный.
Дано: \( p \) — касательная, \( AB \) — диаметр, \( AC = r \), \( p \cap AB = D \).
Доказать: \( \triangle ACD = \frac{\pi}{6} \).
Рассмотрим треугольник \( \triangle AOC \). Радиусы \( OA \) и \( OC \) равны, так как они соединяют центр окружности с её точками. Следовательно, треугольник \( \triangle AOC \) является равнобедренным. Угол \( \angle OCA \) равен \( \angle OAC \), и так как сумма углов треугольника равна \( 180^\circ \), то:
\(
\angle OCA + \angle OAC + \angle AOC = 180^\circ.
\)
Угол \( \angle AOC \) является центральным и опирается на дугу \( AC \), которая составляет половину окружности (так как \( AB \) — диаметр). Следовательно, \( \angle AOC = 60^\circ \). Подставляем значение \( \angle AOC \) в уравнение:
\(
\angle OCA + \angle OAC + 60^\circ = 180^\circ.
\)
Отсюда:
\(
\angle OCA = \angle OAC = \frac{180^\circ — 60^\circ}{2} = 60^\circ / 2 = 30^\circ.
\)
Теперь рассмотрим угол \( \angle BOC \). Этот угол является внешним для треугольника \( \triangle AOC \), а внешний угол равен сумме двух несмежных внутренних углов. Таким образом:
\(
\angle BOC = \angle OCA + \angle OAC = 30^\circ + 30^\circ = 60^\circ.
\)
Рассмотрим треугольник \( \triangle OCD \). Этот треугольник прямоугольный, так как \( OD \) — радиус, а \( p \) — касательная к окружности. Угол между радиусом и касательной равен \( 90^\circ \). Следовательно:
\(
\angle CDO = 90^\circ — \angle BOC = 90^\circ — 60^\circ = 30^\circ.
\)
Теперь рассмотрим треугольник \( \triangle ACD \). В этом треугольнике угол \( \angle A \) равен \( \angle D \), так как оба угла равны \( 30^\circ \) (выше доказано). Следовательно, треугольник \( \triangle ACD \) является равнобедренным.
Кроме того, сумма углов треугольника \( \triangle ACD \) равна \( 180^\circ \). Угол \( \angle CAD \) равен \( \angle CDO \), то есть \( 30^\circ \). Таким образом, треугольник \( \triangle ACD \) имеет углы \( 30^\circ, 30^\circ \) и \( 120^\circ \).
Так как треугольник равнобедренный и его углы соответствуют пропорциям треугольника с углами \( \frac{\pi}{6}, \frac{\pi}{6}, \frac{2\pi}{3} \) в радианах, то площадь треугольника определяется как часть окружности, соответствующая углу \( \frac{\pi}{6} \).
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!