Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 633 Атанасян — Подробные Ответы
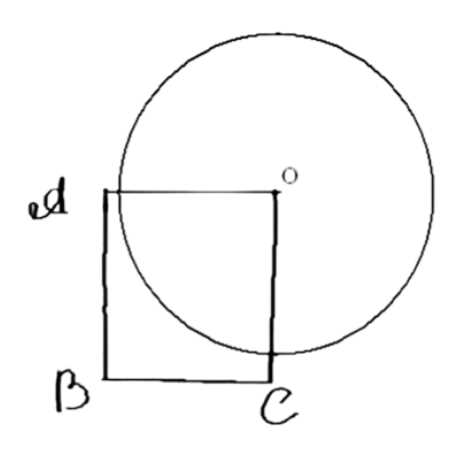
Даны квадрат \( OABC \), сторона которого равна \( 6 \, \text{см} \), и окружность с центром в точке \( O \) радиуса \( 5 \, \text{см} \). Какие из прямых \( OA \), \( AB \), \( BC \) и \( AC \) являются секущими по отношению к этой окружности?
Дано: \(OABC\) — квадрат, \(OA = 6 \, \text{см}\), радиус окружности \(r = 5 \, \text{см}\).
Решение:
1. Прямая \(OA\) проходит через центр окружности, значит она секущая.
2. Прямая \(AB\): расстояние от точки \(O\) до прямой \(AB\) равно \(OA = 6 \, \text{см}\). Так как \(OA > r\), \(AB\) не является секущей.
3. Прямая \(BC\): расстояние от точки \(O\) до прямой \(BC\) равно \(OC = 6 \, \text{см}\). Так как \(OC > r\), \(BC\) не является секущей.
4. Прямая \(AC\): расстояние от точки \(O\) до прямой \(AC\) равно половине диагонали квадрата. Диагональ квадрата:
\[
\sqrt{OA^2 + OA^2} = \sqrt{6^2 + 6^2} = \sqrt{72} = 6\sqrt{2}.
\]
Расстояние:
\[
OD = \frac{\sqrt{72}}{2} = 3\sqrt{2} \approx 4{,}24 \, \text{см}.
\]
Так как \(OD < r\), \(AC\) является секущей.
Ответ: \(OA\) и \(AC\).
Дано: \(OABC\) — квадрат, \(OA = 6 \, \text{см}\), радиус окружности \(r = 5 \, \text{см}\). Требуется определить, какие из прямых \(OA\), \(AB\), \(BC\), \(AC\) являются секущими для окружности.
Решение:
1. Прямая \(OA\) проходит через центр окружности \(O\). Любая прямая, проходящая через центр окружности, пересекает её в двух точках, следовательно, \(OA\) является секущей.
2. Прямая \(AB\) является одной из сторон квадрата и перпендикулярна радиусу \(OA\). Расстояние от точки \(O\) до прямой \(AB\) равно длине радиуса квадрата, то есть \(OA = 6 \, \text{см}\). Так как \(OA > r\), прямая \(AB\) не пересекает окружность и, следовательно, не является секущей.
3. Прямая \(BC\) также является стороной квадрата и перпендикулярна радиусу \(OC\). Расстояние от точки \(O\) до прямой \(BC\) равно длине радиуса квадрата, то есть \(OC = 6 \, \text{см}\). Так как \(OC > r\), прямая \(BC\) не пересекает окружность и, следовательно, не является секущей.
4. Прямая \(AC\) является диагональю квадрата. Чтобы определить, является ли она секущей, нужно найти расстояние от центра окружности \(O\) до диагонали \(AC\). Диагональ квадрата вычисляется по формуле:
\[
\text{Диагональ} = \sqrt{OA^2 + OA^2}.
\]
Подставим значение \(OA = 6 \, \text{см}\):
\[
\text{Диагональ} = \sqrt{6^2 + 6^2} = \sqrt{36 + 36} = \sqrt{72}.
\]
Расстояние от точки \(O\) до диагонали \(AC\) равно половине длины диагонали, то есть:
\[
OD = \frac{\sqrt{72}}{2}.
\]
Упростим выражение:
\[
OD = \frac{\sqrt{72}}{2} = \frac{\sqrt{36 \cdot 2}}{2} = \frac{6\sqrt{2}}{2} = 3\sqrt{2}.
\]
Приблизительно:
\[
OD \approx 3 \cdot 1{,}41 = 4{,}23 \, \text{см}.
\]
Так как \(OD = 4{,}23 \, \text{см} < r = 5 \, \text{см}\), прямая \(AC\) пересекает окружность в двух точках и является секущей.
Ответ: секущими являются прямые \(OA\) и \(AC\).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.