ГДЗ по Геометрии 8 класс Номер 631 Атанасян — Подробные Ответы

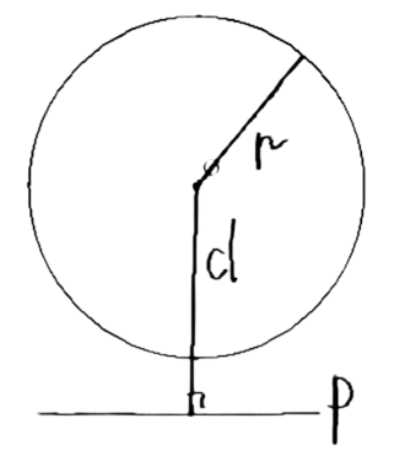
Пусть \( d \) — расстояние от центра окружности радиуса \( r \) до прямой \( p \). Каково взаимное расположение прямой \( p \) и окружности, если:  

а) \( r = 16 \, \text{см}, \, d = 12 \, \text{см} \);  

б) \( r = 5 \, \text{см}, \, d = 4,2 \, \text{см} \);  

в) \( r = 7,2 \, \text{дм}, \, d = 3,7 \, \text{дм} \);  

г) \( r = 8 \, \text{см}, \, d = 1,2 \, \text{дм} \);  

д) \( r = 5 \, \text{см}, \, d = 50 \, \text{мм} \).

Дано: \(d\) — расстояние от центра окружности до прямой, \(r\) — радиус.

а) \(r = 16 \, \text{см}, \, d = 12 \, \text{см}\):
\(r > d\), прямая и окружность пересекаются в двух точках.

б) \(r = 5 \, \text{см}, \, d = 4 \frac{1}{5} \, \text{см}\):
\(r > d\), прямая и окружность пересекаются в двух точках.

в) \(r = 7 \frac{1}{5} \, \text{дм}, \, d = 3 \frac{7}{10} \, \text{дм}\):
\(r > d\), прямая и окружность пересекаются в двух точках.

г) \(r = 8 \, \text{см}, \, d = 12 \, \text{см}\):
\(r < d\), прямая и окружность не пересекаются.

д) \(r = 5 \, \text{см}, \, d = 5 \, \text{см}\):
\(r = d\), прямая и окружность касаются в одной точке.

Дано:
\(d\) — расстояние от центра окружности до прямой,
\(r\) — радиус окружности.

Необходимо определить взаимное расположение прямой и окружности, используя соотношение между \(r\) и \(d\):
1. Если \(r > d\), то прямая пересекает окружность в двух точках.
2. Если \(r = d\), то прямая касается окружности в одной точке.
3. Если \(r < d\), то прямая не пересекает окружность.

Рассмотрим каждый случай:

а) \(r = 16 \, \text{см}, \, d = 12 \, \text{см}\):
Здесь \(r > d\), так как \(16 \, \text{см} > 12 \, \text{см}\).
Следовательно, прямая и окружность пересекаются в двух точках.

б) \(r = 5 \, \text{см}, \, d = 4 \frac{1}{5} \, \text{см}\):
Преобразуем \(d = 4 \frac{1}{5} \, \text{см}\) в десятичную дробь: \(d = 4,2 \, \text{см}\).
Здесь \(r > d\), так как \(5 \, \text{см} > 4,2 \, \text{см}\).
Следовательно, прямая и окружность пересекаются в двух точках.

в) \(r = 7 \frac{1}{5} \, \text{дм}, \, d = 3 \frac{7}{10} \, \text{дм}\):
Преобразуем \(r = 7 \frac{1}{5} \, \text{дм}\) и \(d = 3 \frac{7}{10} \, \text{дм}\) в десятичные дроби:
\(r = 7,2 \, \text{дм}, \, d = 3,7 \, \text{дм}\).
Здесь \(r > d\), так как \(7,2 \, \text{дм} > 3,7 \, \text{дм}\).
Следовательно, прямая и окружность пересекаются в двух точках.

г) \(r = 8 \, \text{см}, \, d = 1,2 \, \text{дм}\):
Преобразуем \(d = 1,2 \, \text{дм}\) в сантиметры: \(d = 12 \, \text{см}\).
Здесь \(r < d\), так как \(8 \, \text{см} < 12 \, \text{см}\).
Следовательно, прямая и окружность не пересекаются.

д) \(r = 5 \, \text{см}, \, d = 50 \, \text{мм}\):
Преобразуем \(d = 50 \, \text{мм}\) в сантиметры: \(d = 5 \, \text{см}\).
Здесь \(r = d\), так как \(5 \, \text{см} = 5 \, \text{см}\).
Следовательно, прямая и окружность касаются в одной точке.

Таким образом, выполнено полное решение с учетом всех возможных случаев.