ГДЗ по Геометрии 8 класс Номер 630 Атанасян — Подробные Ответы

Постройте треугольник по стороне и медианам, проведённым к двум другим сторонам.

Дано: сторона треугольника \(AB\), медианы \(a_1\) и \(b_1\). Построить треугольник \(\Delta ABC\).

Построение:
1. Разделить отрезки \(a_1\) и \(b_1\) на три равные части.
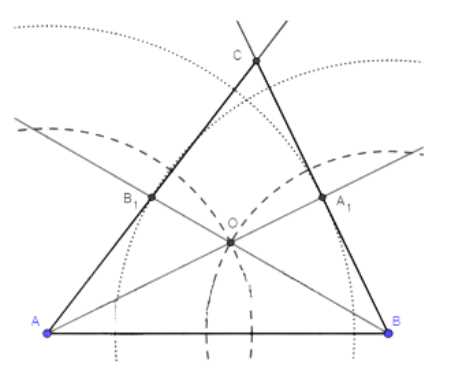
2. Построить окружности из точки \(A\) с радиусом \(\frac{2}{3}a_1\) и из точки \(B\) с радиусом \(\frac{2}{3}b_1\). Пересечение окружностей — точка \(O\).
3. Провести лучи \(AO\) и \(BO\), отметить на них точки \(A_1\) и \(B_1\), где \(AA_1 = a_1\), \(BB_1 = b_1\).
4. Построить лучи \(AB_1\) и \(BA_1\). Их пересечение — точка \(C\).
5. Соединить точки \(A\), \(B\) и \(C\).

Дано:
Сторона треугольника \(AB\), медианы \(a_1\) и \(b_1\). Требуется построить треугольник \(\Delta ABC\).

Решение:

1. Разделим отрезки \(a_1\) и \(b_1\) на три равные части. Для этого:
— Отметим точки деления на отрезке \(a_1\), чтобы каждая часть имела длину \(\frac{a_1}{3}\).
— Аналогично отметим точки деления на отрезке \(b_1\), чтобы каждая часть имела длину \(\frac{b_1}{3}\).

2. Построим окружности:
— Из точки \(A\) проведем окружность с радиусом \(\frac{2}{3}a_1\).
— Из точки \(B\) проведем окружность с радиусом \(\frac{2}{3}b_1\).
— Найдем точку пересечения этих окружностей и обозначим её как точку \(O\).

3. Построим лучи \(AO\) и \(BO\):
— На луче \(AO\) отметим точку \(A_1\), такую, что \(AA_1 = a_1\).
— На луче \(BO\) отметим точку \(B_1\), такую, что \(BB_1 = b_1\).

4. Построим лучи \(AB_1\) и \(BA_1\):
— Продлим луч \(AB_1\) из точки \(A\) через точку \(B_1\).
— Продлим луч \(BA_1\) из точки \(B\) через точку \(A_1\).
— Найдем точку пересечения этих лучей и обозначим её как точку \(C\).

5. Соединим точки \(A\), \(B\) и \(C\):
— Проведем отрезки \(AC\), \(BC\) и \(AB\), которые образуют треугольник \(\Delta ABC\).

Таким образом, построение треугольника завершено.