ГДЗ по Геометрии 8 класс Номер 629 Атанасян — Подробные Ответы

Постройте треугольник, если даны середины его сторон.

Для построения треугольника ΔАВС по серединам его сторон выполняем следующие шаги:

1. Соединяем точки A₁C₁, C₁B₁ и A₁B₁ отрезками.
2. Через каждую из точек A₁, B₁, C₁ проводим прямые, параллельные противоположным сторонам.
3. В точках пересечения этих прямых отмечаем вершины треугольника A, B и C.

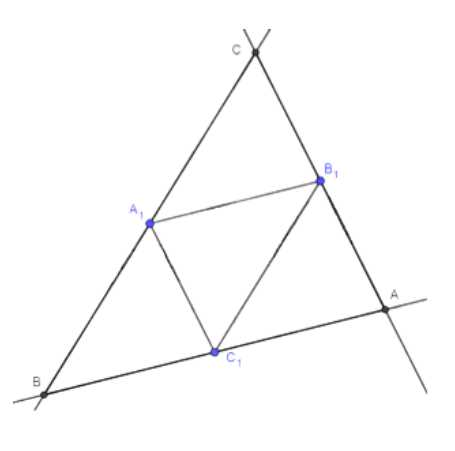
Для построения треугольника \(\Delta ABC\) по заданным серединам его сторон \(A_1, B_1, C_1\), выполняем следующие шаги:

1. Соединяем точки середины сторон:
Соединяем точки \(A_1\) и \(C_1\), \(C_1\) и \(B_1\), а также \(A_1\) и \(B_1\) отрезками. Получаем треугольник \(A_1B_1C_1\), который является срединным треугольником исходного треугольника \(\Delta ABC\).

2. Проводим прямые, параллельные противоположным сторонам:
Через каждую точку \(A_1, B_1, C_1\) проводим прямую, параллельную противоположному отрезку:
— Через точку \(A_1\) проводим прямую, параллельную стороне \(B_1C_1\).
— Через точку \(B_1\) проводим прямую, параллельную стороне \(A_1C_1\).
— Через точку \(C_1\) проводим прямую, параллельную стороне \(A_1B_1\).

3. Определяем вершины треугольника:
Находим точки пересечения проведенных прямых:
— Пересечение прямых, проходящих через \(A_1\) и \(B_1\), дает вершину \(C\).
— Пересечение прямых, проходящих через \(B_1\) и \(C_1\), дает вершину \(A\).
— Пересечение прямых, проходящих через \(A_1\) и \(C_1\), дает вершину \(B\).

4. Проверка правильности построения:
Убедимся, что точки \(A, B, C\) являются вершинами треугольника, стороны которого проходят через середины \(A_1, B_1, C_1\), и что треугольник \(\Delta ABC\) соответствует условию задачи.

Таким образом, треугольник \(\Delta ABC\) построен.