
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 627 Атанасян — Подробные Ответы
Дан треугольник \( ABC \). Постройте треугольник \( A_1B_1C_1 \), подобный треугольнику \( ABC \), площадь которого в два раза больше площади треугольника \( ABC \).
Дано:
Построить треугольник \(\triangle A_1B_1C_1 \sim \triangle ABC\), чтобы площадь \(S_{A_1B_1C_1}\) была в два раза больше площади \(S_{ABC}\).
Решение:
Так как треугольники подобны, то отношение их площадей равно квадрату коэффициента подобия:
\(
\frac{S_{A_1B_1C_1}}{S_{ABC}} = k^2.
\)
Из условия задачи:
\(
\frac{S_{A_1B_1C_1}}{S_{ABC}} = 2, \quad k^2 = 2, \quad k = \sqrt{2}.
\)
Следовательно, стороны треугольника \(A_1B_1C_1\) пропорциональны сторонам треугольника \(ABC\):
\(
A_1B_1 = \sqrt{2}AB, \quad B_1C_1 = \sqrt{2}BC, \quad A_1C_1 = \sqrt{2}AC.
\)
Для построения треугольника:
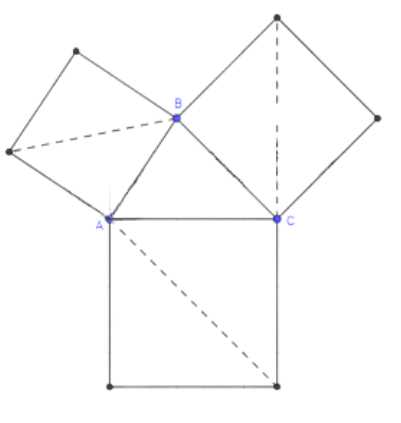
1. На каждой стороне треугольника \(ABC\) строим квадрат. Диагонали квадратов будут равны сторонам треугольника \(A_1B_1C_1\).
2. Проводим прямые, параллельные сторонам \(AB\) и \(AC\), чтобы их пересечение определило вершину \(A_1\).
3. Отмечаем точки \(B_1\) и \(C_1\) на диагоналях квадратов, соответствующих сторонам \(AB\) и \(AC\).
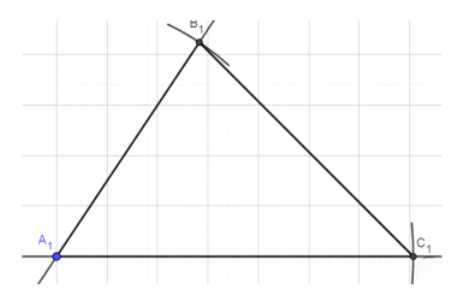
4. Соединяем точки \(A_1\), \(B_1\) и \(C_1\), получая треугольник \(A_1B_1C_1\).
Таким образом, треугольник \(A_1B_1C_1\) подобен треугольнику \(ABC\), а его площадь в два раза больше.
Дано: треугольник \( \triangle ABC \). Требуется построить треугольник \( \triangle A_1B_1C_1 \), подобный треугольнику \( \triangle ABC \), такой, что его площадь \( S_{A_1B_1C_1} \) в два раза больше площади \( S_{ABC} \).
Решение:
1. По условию задачи треугольники \( \triangle A_1B_1C_1 \) и \( \triangle ABC \) подобны. Из свойства подобных треугольников известно, что отношение их площадей равно квадрату коэффициента подобия:
\(
\frac{S_{A_1B_1C_1}}{S_{ABC}} = k^2,
\)
где \( k \) — коэффициент подобия.
2. Подставим условие задачи \( \frac{S_{A_1B_1C_1}}{S_{ABC}} = 2 \):
\(
k^2 = 2.
\)
Отсюда находим коэффициент подобия:
\(
k = \sqrt{2}.
\)
3. Так как коэффициент подобия \( k = \sqrt{2} \), то стороны треугольника \( \triangle A_1B_1C_1 \) пропорциональны сторонам треугольника \( \triangle ABC \) с коэффициентом \( \sqrt{2} \):
\(
A_1B_1 = \sqrt{2} \cdot AB, \quad B_1C_1 = \sqrt{2} \cdot BC, \quad A_1C_1 = \sqrt{2} \cdot AC.
\)
4. Для построения треугольника \( \triangle A_1B_1C_1 \) выполним следующие шаги:
а) На каждой стороне треугольника \( \triangle ABC \) построим квадрат. Например, для стороны \( AB \) строим квадрат \( ABDE \), где \( AB \) — одна из сторон квадрата, а вершины \( D \) и \( E \) находятся вне треугольника. Аналогично строим квадраты на сторонах \( BC \) и \( AC \).
б) Диагонали квадратов будут равны сторонам нового треугольника \( \triangle A_1B_1C_1 \), так как диагональ квадрата равна \( \sqrt{2} \) умножить на длину его стороны.
в) Проводим прямые, параллельные сторонам \( AB \) и \( AC \), так чтобы их пересечение определило вершину \( A_1 \).
г) Отмечаем точки \( B_1 \) и \( C_1 \) на диагоналях квадратов, соответствующих сторонам \( AB \) и \( AC \).
д) Соединяем точки \( A_1 \), \( B_1 \) и \( C_1 \), получая треугольник \( \triangle A_1B_1C_1 \).
5. Проверим, что площадь нового треугольника в два раза больше площади исходного. Так как коэффициент подобия \( k = \sqrt{2} \), то:
\(
S_{A_1B_1C_1} = k^2 \cdot S_{ABC} = 2 \cdot S_{ABC}.
\)
Ответ: треугольник \( \triangle A_1B_1C_1 \) построен, он подобен треугольнику \( \triangle ABC \), а его площадь в два раза больше площади исходного треугольника.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!