ГДЗ по Геометрии 8 класс Номер 624 Атанасян — Подробные Ответы

Докажите, что медианы треугольника разбивают его на шесть треугольников, площади которых попарно равны. 

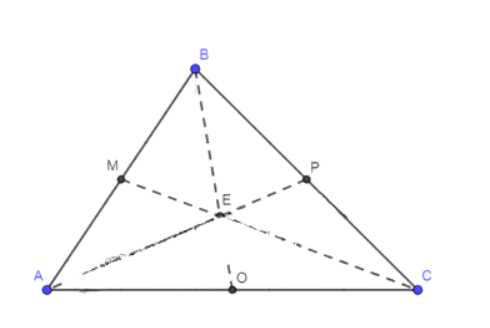
Дано: \(\triangle ABC\), медианы \(AP, BO, CM\).
Доказать: \(S_{AEM} = S_{BEM}, S_{AEO} = S_{COE} = S_{PEC} = S_{BEP}\).

Решение:
1) По определению медиан: \(BP = PC, AO = OC, AM = MB\).

2) Пусть площадь \(\triangle ABC\) равна \(S\). Тогда:
\(
S_{ABO} = \frac{1}{2} AO \cdot h, \quad S_{OBC} = \frac{1}{2} OC \cdot h.
\)
Так как \(AO = OC\), то \(S_{ABO} = S_{OBC} = \frac{S}{2}\).

\(
S_{ABP} = \frac{1}{2} BP \cdot h, \quad S_{APC} = \frac{1}{2} PC \cdot h.
\)
Так как \(BP = PC\), то \(S_{ABP} = S_{APC} = \frac{S}{2}\).

\(
S_{AMC} = \frac{1}{2} AM \cdot h, \quad S_{MBC} = \frac{1}{2} MB \cdot h.
\)
Так как \(AM = MB\), то \(S_{AMC} = S_{MBC} = \frac{S}{2}\).

3) Из условия:
\(
S_{ABP} + S_{AMC} = S_{AME} + S_{EPC} = S.
\)
Подставляя значения:
\(
\frac{S}{2} + \frac{S}{2} = S = S_{EPC} + S_{AME}.
\)
Следовательно:
\(
S_{AME} = S_{EPC}.
\)

4) Учитывая равенство высот для медиан:
\(
S_{AEM} = S_{MBE}, \quad S_{EBP} = S_{EPC}, \quad S_{AEO} = S_{COE}.
\)
Таким образом, доказано, что:
\(
S_{AEM} = S_{BEM}, \quad S_{AEO} = S_{COE} = S_{PEC} = S_{BEP}.
\)

Дано: треугольник \( \triangle ABC \). Медианы \( AP \), \( BO \), \( CM \).
Доказать: \( S_{AEM} = S_{BEM} \), \( S_{AEO} = S_{COE} = S_{PEC} = S_{BEP} \).

Решение:
1. Рассмотрим свойства медиан.
Медиана \( AP \) делит сторону \( BC \) на два равных отрезка, то есть \( BP = PC \).
Медиана \( BO \) делит сторону \( AC \) на два равных отрезка, то есть \( AO = OC \).
Медиана \( CM \) делит сторону \( AB \) на два равных отрезка, то есть \( AM = MB \).

2. Пусть площадь треугольника \( \triangle ABC \) равна \( S \).
Тогда каждая медиана делит треугольник на два треугольника равной площади. Например:
\( S_{ABO} = S_{OBC} = \frac{S}{2} \), так как медиана \( BO \) делит треугольник \( \triangle ABC \) на два равных по площади.

Аналогично:
\( S_{ABP} = S_{APC} = \frac{S}{2} \), так как медиана \( AP \) делит треугольник \( \triangle ABC \) на два равных по площади.

И также:
\( S_{AMC} = S_{MBC} = \frac{S}{2} \), так как медиана \( CM \) делит треугольник \( \triangle ABC \) на два равных по площади.

3. Рассмотрим площади внутри треугольника.
Площадь треугольника \( \triangle ABC \) можно представить как сумму площадей треугольников \( \triangle ABP \) и \( \triangle APC \):
\(
S = S_{ABP} + S_{APC}.
\)
При этом каждая из этих площадей равна \( \frac{S}{2} \).

Аналогично, площадь \( S \) можно представить как сумму площадей треугольников \( \triangle AMC \) и \( \triangle MBC \):
\(
S = S_{AMC} + S_{MBC}.
\)
Каждая из этих площадей также равна \( \frac{S}{2} \).

4. Рассмотрим точки пересечения медиан.
Точки пересечения медиан (например, точка \( E \)) делят каждую медиану в отношении \( 2:1 \), считая от вершины треугольника. Это свойство гарантирует, что треугольники, образованные точкой пересечения медиан, будут равны по площади.

Например, площадь треугольника \( \triangle AEM \) равна площади треугольника \( \triangle BEM \), так как высота из точки \( E \) к стороне \( AB \) общая, а отрезки \( AM \) и \( MB \) равны. Таким образом:
\(
S_{AEM} = S_{BEM}.
\)

Аналогично, площадь треугольника \( \triangle AEO \) равна площади треугольника \( \triangle COE \), так как высота из точки \( E \) к стороне \( AC \) общая, а отрезки \( AO \) и \( OC \) равны. Таким образом:
\(
S_{AEO} = S_{COE}.
\)

5. Рассмотрим площади треугольников \( \triangle PEC \) и \( \triangle BEP \).
Эти треугольники также имеют общую высоту из точки \( E \) к стороне \( BC \), а отрезки \( BP \) и \( PC \) равны. Таким образом:
\(
S_{PEC} = S_{BEP}.
\)

6. Итоговое заключение:
Все доказанные равенства площадей внутри треугольника \( \triangle ABC \):
\(
S_{AEM} = S_{BEM}, \quad S_{AEO} = S_{COE} = S_{PEC} = S_{BEP}.
\)
Доказательство завершено.